TerraceM

Backgrounds

Backgrounds of marine and lacustrine terraces

Wednesday 19 August 2015 at 07:38 am.

(Modified fragments and figures from Jara Muñoz et al., 2016, Geosphere)

The conjugated effects of tectonic uplift, sea level variations and surface erosive processes are responsible to shape the coastal landscape. Marine terraces are ephemeral coastal landforms portrayed by flat and smooth surfaces or paleo-platforms that dip seaward, bounded by scarps or paleo-cliffs inland that delimitate each terrace level (Fig. 1A and B). Marine terraces have been sculpted in the landscape during sea-level high-stands (Lajoie, 1986; Anderson et al., 1999), forming wave-cut or wave-built terraces, rasas, strand-flats, and compound paleo-coasts (e.g. Guilcher et al., 1986; Regard et al., 2010; Keskin et al., 2011; Pedoja et al., 2014; Jara-Muñoz and Melnick, 2015). During episodes of sea-level rise or still stands, wave-erosion processes in rocky coasts are enhanced, resulting in the carving of wave-cut platforms above the bedrock due to rapid cliff retreat (Challinor, 1949; Sunamura, 1983; Anderson et al., 1999; Trenhaile, 2000) (Fig. 2A). During sea-level low-stands terraces may be dismantled by the effects of river incision and/or paleo-cliff diffusion, or covered by eolian sediments (Figs. 2B, 2C and 3A). After tens of thousands of years, surface uplift may preserve these snapshots of past sea-level positions, creating staircase sequences of marine terraces.

The elevation of marine terraces has been usually estimated from its surface morphology and is used as a proxy for the calculation of the amount of uplift since the terrace was formed. There are several extended methods and markers that have been used to estimate terrace elevations (Fig. 2D), for instance by manually picking slope changes that form at the cliff foot along topographic profiles, commonly referred to as the terrace inner edge (e.g. Armijo et al., 1996; Saillard et al., 2009; Regard et al., 2010; Roberts et al., 2013), or with more sophisticated methods such as isolating terrace platform surfaces from a combined analysis of the slope and roughness of the terrain from high-resolution DTMs (i.e. Palamara et al., 2007; Bowles and Cowgill, 2012). However, terrace elevations estimated from different markers may result in disparate estimates and large ranges in the derived uplift rates.

(Figure 1)

According to Lajoie (1986), the shoreline angle defines the elevation of the sea level at the time of terrace formation; this point is located at the based of the cliff in modern actively forming terraces. In emerged wave-cut terraces, it should be located close to the intersection between paleo-cliff and paleo-platform (Fig. 2D). Shoreline angles can be correlated with the maximum sea-level position during a defined high-stand period. The uplift rate (Ur) may be estimated from:

Ur = (Te-Sl)/t (Eq. 1, Lajoie, 1986)   

Ur=Te/t (Eq. 2, Pedoja et al., 2008)

Where, Te is the present-day terrace elevation, and Sl the sea-level position at the time of formation (t), the total uplift is then calculated from the difference between Te and Sl divided by t. If we assume Sl=0, following Pedoja et al. (2008), we can discard errors attributed to sea-level corrections obtaining a relative uplift rate respect to present sea-level, but a substantial bias may be introduced in areas of low tectonic uplift. Clearly from both equations uplift rates estimated for younger marine terraces will strongly depend on the precision of the terrace elevation measurements (Te).

The difficulty of estimating the terrace elevation lies in the correlation of the deformation markers in time and space. For instance, the inner edge calculated from slope maps (e.g. Palamara et al., 2007) often represents the contact between the colluvium wedge and the paleo-cliff, which is systematically located at higher elevation than the shoreline angle (e.g. Matsu'ura et al., 2014) (Fig. 2D). Along these lines, surface classification models (SCM) (e.g. Bowles and Cowgill, 2012) that have been used to map the elevation of terrace treads or paleo platforms will tend to underestimate uplift rates as these makers usually form below mean sea level, and before the sea-level high-stand peak when the cliff actively retreats (Fig. 2D). Thus, geomorphic markers may lead to disparate uplift rates with underestimated uncertainties. Therefore, and following the definition of Lajoie (1986), we consider the shoreline angle as the most adequate marker to use for estimating uplift rates from terrace elevation data, as it can be compared directly with the position of sea level.

(Figures 2 A-D)

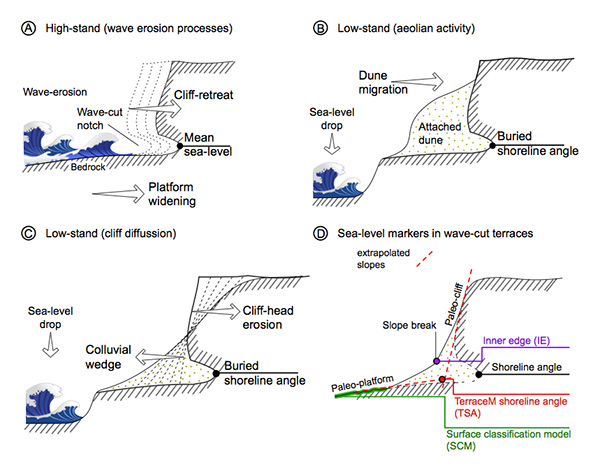
The shoreline angle of emerged marine terraces is commonly concealed when the paleo-cliffs and/or paleo-platforms are affected by a) scarp diffusion, b) river incision, or c) eolian accumulation processes (Figs. 2B and 2C and 3A to 3D):

a) Diffusion processes in scarps are responsible to obscure the shoreline angle position, however they also allow estimating the geomorphic age (Kt), as is demonstrated by several studies using erosive features such as fault and terrace scarps (e.g. Wallace, 1977; Bucknam and Anderson, 1979; Hanks et al., 1984; Avouac, 1993). Scarp diffusion processes have been modeled by (Hanks et al., 1984) using the equations below and applied to marine terraces based in the assumption that mass transport resulting from erosional processes occurs exclusively in the downhill direction at a rate (M) proportional to the local topography gradient (δu/δx). The mass conservation holds a local scale and is defined by the constant of proportionality (K), which is equal to the diffusivity (k) divided by the density of the bedrock (ρ). The material removed from the scarp top and accumulated at the base is thus adjusted symmetrically along the scarp profile over time implying that the shoreline angle might be covered by an increasing amount of colluvium as the cliff slope progressively decreases (Fig. 2C). The geomorphic age of the paleo-cliff (in m² units) is obtained from the error function between topography and diffusion models.

Mass transport equation (Hanks, 1984):                   M= -K(δu/ δx)  Eq. (3)

Proportionality constant (Hanks, 1984):       K=k / ρ  Eq. (4)

b) River incision is adjusted by changes in the erosive base level, which in coastal regions is commonly the sea level (Bishop et al., 2005). Thus, most of the river incision observed in terrace surfaces occurred during sea-level lowstands, when the stream power was higher (Talling, 1998). Cycles of sea-level variations are expressed as retreating knick points, which transmit signals of base level fall along river networks (Crosby and Whipple, 2006; Loget and Van Den Driessche, 2009). Incision generally increases with terrace age progressively dismantling the morphology of both paleo-platforms and paleo-cliffs (e.g. Fig. 1 and 3A).

c) Sediment transport along coastal regions is a dynamic process, resulting in either formation of rocky platforms or sandy beaches depending of the shore morphology, the amount of sediments, tidal range, and wave exposure (e.g. Trenhaile, 2001; Ruz and Meur-Ferec, 2004; Twidale et al., 2005). Eolian transport usually increases during sea-level low-stands due the retreat of the coastal system (e.g. Bradley and Addicott, 1968; Cantalamessa and Di Celma, 2004; Masselink et al., 2014). Sediment remobilization is adjusted by local winds and sediment availability, forming coastal dunes systems that usually migrate inland (Bailey and Bristow, 2004; Carr et al., 2006). Such eolian sediments may cover terrace platforms and occasionally climb across the paleo-cliff (Fig. 2B), forming a sedimentary body that may obscure terrace morphology and bury the shoreline angle (Figs. 2B, 3B).

The aforementioned features of marine terraces have been compared worldwide in order to understand their origin and the genesis of uplifted paleo-coasts in the context of the history of sea-level changes. (e.g. Pedoja et al., 2014). However, the influence of erosion and accumulation processes affecting marine terraces and their bias on derived uplift and deformation rates has not been yet fully addressed quantitatively. In order to quantify these processes taking advantage of recent availability of high-resolution topography, we have developed TerraceM, which allows to: 1) Explore different methodologies to quantify and isolate erosive and depositional processes that usually mask the position of the shoreline angle; 2) Extract shoreline angles continuously along terrace exposures using a large number of profiles and 3) quickly visualize and export the results to other software platforms.

(Figure 3 A-B)

(Modified fragments and figures from Jara Muñoz et al., 2016, Geosphere)