Grandes Problemas Clásicos de la Geometría

De entre los problemas geométricos que los griegos intentaron resolver y no lo consiguieron, hay tres que han pasado a la historia pero citaremos solo dos y que, repetidamente a lo largo de los siglos, se ha intentado hallar una solución hasta que, en el siglo XIX, se demostro facilmenteque eran irresolubles con regla y compás. Estos problemas son muy fáciles de comprender y aparentemente no muy dificiles de conseguir su solución. Considero interesante decribirlos someramente, aparte su interes histórico, porque nos permiten entender como el álgebra ayudo a resolver estos problemas geométricos.

(A) Trisección de un ángulo

Se trata de conseguir dividir (con regla y compás) un ángulo en tre partes de manera exacta. Una solución aproximada es muy facil de conseguir con un tranportador: se mide el ángulo, se divide en tres y a continuacion se procede a trazar el ángulo correspondiente.

Hay que observar que, en ocasiones, algunos ángulos se pueden trisectar sin ninguna dificultad, como se puede observar facilmente en la triseccion del ángulo de 180º, 90º o bien como lo hemos hecho anteriormente con el ángulo central del pentagono regular (72º) para dibujar un polígono de 15 lados. El problema clásico se refiere al caso genral de un ángulo cualquiera.

Tras muchos fracasos llegaron a obtener una solución ayudandose de un aparato que les permitia la division de manera efectiva y sencilla. Éste consisti en algo parecido a una L en la que los dos brazos tienen la misma anchura (arbitraria) y el lado pequeño tenia una longitud triple que la anchura y acababa en un cuadrante de circunferencia.

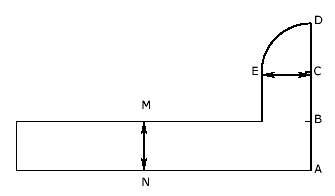
Siendo AB=BC=CD=CE=MN=a y DE es un arco de circunferenciacon centro en C. Para dividir un ángulo AOB en tres partes, se utilizaba este instrumento de la siguiente manera:

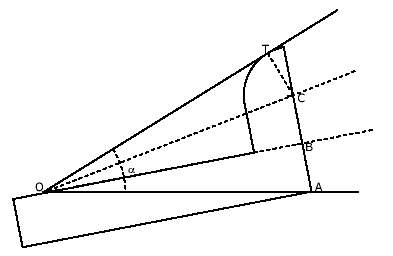
Se desplazaba y giraba sobre el ángulo de tal manera ue qudase con el vértice del ángulo en un punto de la parte superior del mango y al mismo tiempo, A debia quedar situado en un lado del ángulo, siendo el otro lado tangente interior al arco DE. Los tres triángulos OAB, OBC y OCT son rectángulos y tienen la misma hipotenusa y el cateto menor, luego los ángulos son iguales a la tercera parte de .

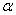No obstante la exigencia matemática de los griegos iba más alla de una aproximacion o solución técnica y el hecho de que el apartado se tuviera que apoyar sobre un punto que no resultaba perfectamente determinado con procedimientos geométricos no les satisfizo, po lo que siguieron buscando una solucion en la que sólo intervinieran la regla y el compas. cosa que no consiguieron.

(B) Duplicacion del Cubo

Consiste en la construccion, con regla y compás, de un cubo cuyo volumen sea el doble del otro conocido. para simplificar, se puede suponer que el primero tiene lado unidad, con lo que el problema se reduce a buscar la forma de contruir un segmento que sea arista del cubo de volumen 2, o sea, de longitud 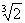. Aparentemente tambien es un problema accesible pero, por mas que se intento, la solución siempre se resistía.

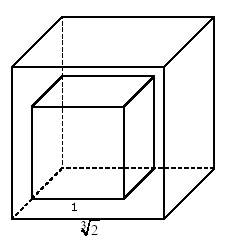
La solución de estos problemas se intentó de forma más o menos continua hasta bien entrado el siglo XIX que se demostro que las soluciones no esxistian. Para entender muy supuestamente como se llego a demostrar, podemos decir que se puede demostrar que un número es constructible (es decir, se puede construir con regla y compás un segmento cuya longitud sea el número dado) si es solución de una ecuacuación polinómica de coeficientes racionales cuo grado sea uno, dos o una potencia de dos.

Asi el problema geometrico se transforma en un problema algebraico en el que se estudia si un determinado número puede ser o no ser solución de una ecuación del citado tipo.

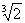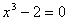En el caso de la duplicacion del cubo, la ecuación mas sencilla (de menor grado) que tiene como solucion es de tercer grado por lo que al no ser una potencia de dos no se puede construir un segmento cuya medida sea 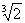y el problema no se puede resolver.