1 Sobre un edificio de 30 m de altura hay un cartel anunciador de 10 m de alto. ¿A qué distancia del edificio verá el cartel bajo un ángulo máximo un "diminuto" peatón que camina perpendicularmente a la fachada?
Este problema corresponde a uno de "Máximos y minimos", una ayuda ideal es el concepto de derivadas. Pero si nos fijamos y reflexionamos un poco en los conceptos geométricos que subyacen en el problema, puede transformarse en otro cuta solución es muy sencilla.
Pensemos en el ángulo inscrito (P5). Si tenemos un segmento fijo AB y consideramos una circunferencia que pase por estos dos puntos, el ángulo inscrito que determina su arco será tanto mayor cuanto más pequeña sea la circunferencia.
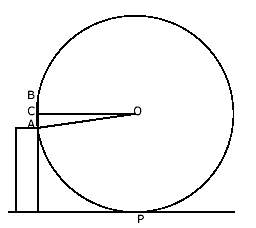
Así podemos considerar que el ángulo bajo el que ve el peatón el anuncio es el ángulo inscrito del arco que determina éste. Y para que sea lo mas grande posible, la circunferencia debera ser tangente al suelo (si fuera más pequeña no lo cortaria), luego el radio OP sera de 35 m, y el triángulo AOC (AO=OP=35, AC=1/2AB) resulta por teorema de Pitágoras:
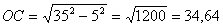
2 Calcular el volúmen de un tetraedro del que se conocen sus aristas.
Supongamos que la base es un triángulo de lados 21, 28 y 25 cm y las caras laterales tienen medida: 21, 24, 22 ; 28, 24, 26 y 25, 26, 22 cm
Sabemos que su volúmen viene dado por la conocida fórmula:
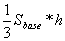
La base se puede representar y calcular fácilmente su área. El problema lo tenemos con la altura por la dificultad de representar los objetos del espacio en el plano de forma precisa, pero podemor realizar un modelo a escala construyendo su desarrollo.
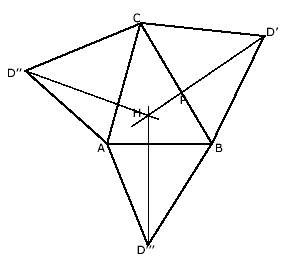
Dibujamos el triángulo de la base y continuamos con las caras laterales utilizando cada uno de los lados de la base.
La cara lateral BCD la hemos "abatido" sobre el plano haciendola pivotar sobre el lado BC de la base, asi el recorrido del vértice superior D estará en un plano perpendicular a BC. Por lo tanto, la proyeccion sobre la base del vértice superior se encontrara sobre la recta perpendicular al lado BC que pasa por D' y lo mismo ocurrira con D'' y D'''. Sea H dicha proyección y P la intersección de AB con D'H. El triángulo DHP es rectángulo en H, y de este conocemos la base y la hipotemusa (las podemos medir en el dibujo), luego podemos representarlo (vease grande problemas clásicos) y calcular su altura que sera al mismo tiempo la altura del tetraedro.
|