Elementos Generales

En la Geometría de la regla y el compás se construyen los ángulos de manera exacta por procedimientos geométricos, lo que exige suponer que las rectas son lineas sin espesor. En la vida real esto es imposible, pues por mas fina que sea la punta del lapiz con que se dibujen siempre tienen un determinado espesor, asi los valores que podemos obtener nunca pueden ser exactos sino aproximaciones mas o menos buenas, en funcion de la exactitud de los elementos de construccion y dela habilidad o destreza con que los hayamos trazado.

En el estudio de un problema geometrico utilizaremos el transportador para construir y medir los ángulos con comodidad, aunque no podar constituir nunca un elemento de demostración. La exactitud geométrica se obtiene siempre por razonamientos y cálculos geométricos (por ejemplo, aplicando el Teorema de Pitágoras). de igual manera, no se puede sustituir por cualquier número decimal si no es para obtener un valor aproximado.

Para duplicar un ángulo de manera exacta, se puede trazar una circunferencia con centro en el vertice del ángulo y un determinado radio y, a continuacion, midiendo con el compas la medida del arco que determina se podri copiar el otro punto sin mas dificultades.

Hay ocasiones en las que no disponemos de un transportador y necesitamos hacer un esboso para estudiar un problema. En estoas casos se puede trazar un ángulo de un determinado valor con un error muy pequeño sin mas que dividir en dos o tres partes un ánglo conocido.

1 Mediatriz de un segmento AB

Se deben trazar dos circunferencias con el mismo radio en centros en cada uno de los extremos del segmento (A y B) y, luego, basta con unir los puntos de interseccion (P1 y Q2)

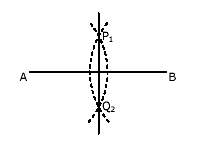
Este procedimiento nos permite hallar tambien el punto medio del segmento AB.

2 Perpendicular a una recta por un punto P exterior a ella.

Se traza una circunferencia con centro en P y con el suficiente radio para que intersecte a la recta en dos puntos A y B. La mediatriz de A y B es la recta buscada.

3 Perpendicular a una recta por un punto de ella.

El comentario anterior tambien sirve para este caso

4 Triángulo conocidos sus lados.

Se traza un segmento mayor en horizontal y, a continuacion, una circunferencia en uno de sus extremos con radio el segundo lado y otra con centro en el otro extremo y radio el tercer lado. La intersección de éstas es, evidentemente, el tercer vértice.

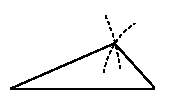
Se ve facilmente que, que para que se pueda formar el triángulo, se debe cumplir la conocida desigualdad triángular: la suma de dos de los lados del triángulo ha de ser siempre mayor que el tercero:

a<b+c

5 Triángulo rectángulo conociendo un cateto y la hipotemusa.

Se traza el cateto horizontal y por uno de sus extremos una recta perpendicular y una circunferencia con centro en el otro extremo y radio la hipotemusa.

otra forma seria dibujar la hipotemusa en horizontal, la circunferencia que la tiene como diámetro, y una circunferencia con centro en un extremo y radio el cateto conocido. la interseccion de las circunferencia es el tercer vértice (aplicar P6= preliminares 6).

6 Triángulo del que se conoce un lado y dos ángulos.

El tercer ángulo se halla facilmente (por P1 la suma de los tres es de 180º), por lo que se puede suponer que los ángulos conocidos son los de los extremos del lado. Se traza en horizontal el lado y en sus extremos los ángulos, donde se corten los lados de estos tenemos el tercer vértice.

7 Cuadrado de lado conocido.

Dibujado un lado en horizontal se levantan verticales por sus extremos y trazando circunferencias de radio igual al lado y centro de los extremos de aquel, obtenemos los otros vertices en las intersecciones respectivas.

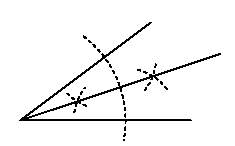
8 Bisectriz de un ángulo.

Basta trazar una circunferencia cualquiera con centro en el vértice del ángulo ymarcar los puntos interseccion con los lados del ángulo. la mediatriz de este segmento es la bisectriz buscada (se considera solo una semirecta que parte del vértice).

9 Paralela a una recta r por un punto P exterior a ella.

Se traza la perpendicular a r por P y, a continuacion su propia perpendicular (aplicar 3).

10 Determina el centro de una circunferencia.

Se marcan tres puntos de la misma y, acto seguido, se trazan las madiatrices de dos de los segmentos que determinen. Su interseccion es el centro.

11 Circunferencia que pasa por tres puntos.

Con el procedimiento anterior se halla el centro de la circunferencia buscada, y abriendo el compas hasta uno de los puntos tendremos el radio.

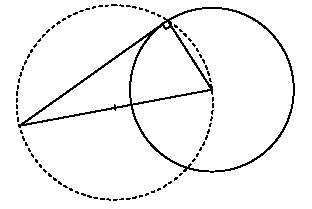
12 Trazar la tangente a una circunferencia desde un punto exterior a ella.

se pueden aplicar P6 y P7, luego bastará con dibujar la circunferencia cuyo diámetro sea el punto y el centro de la dada. El punto de tangencia se encuentra donde se corten las circunferencias.

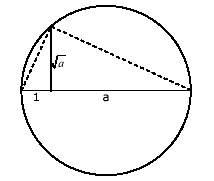
13 Segmento que nos dé la raiz cuadrada de un número.

Dibujamos un segmento horizontal de longitud 1+a y trazamos la circunferencia cuyo diametro es dicho segmento. por el punto que dista 1 desde uno de los extremos se levanta la perpendicular hasta encontrar la circunferencia.

Este segmento es precisamente la raiz cuadrada de a (basta aplicar P6 y el teorema de la altura P4).

Video

Se adjunta un video para que se pueda ver la realizacion de cada una de las construcciones

(codigo del video)