Análisis y síntesis

Como normas de carácter general, para resolver los problemas de construcción se pueden tomar en consideracion las siguientes:

• Conviene estudiar si en el problema existen elementos que nos pueden ayudar como simetrías, semejanzas, etc. En este caso, el problema suele simplificarse mucho.
• Si los elementosqie nos dan son genéricos no conviene presuponer o tomar los miscos valores, porque pudiéramos encontrarnos con un caso particular que enmascarara la generalidad.
• En bastantes ocaciones, un procedimiento vastante útil para comprender y averiguar comó se puede obtener la solución de suponer que ya se tiene ésta, y sobre su dibujo esbozado intentar determinar elementos o relaciones que nos permitan entender o adivinar cuál es el camino a recorrer. así, se debe realizar un recorrido inverso o marcha atrás, esto es precisamente lo que los griegos llamaban el análisis para, finalmente, llegar a la sístesis.
• Algunos problemas complicados pueden presentar varias posibilidades de ataque para poder resolverlos, en estos casos conviene investigar un poco de cada una por ver cuál de todas ellas ofrencen garantías de viabilidad. El hecho de investigar a fondo de una determinada opción no nos asegura que nos vaya a dar resultados, en ese caso habríamos dedicado mucho tiempo sin obtener ningún fruto. El ejemplo del ovillo de lana o de la cuerda todo liado es bastante ilustrativo: conviene tirar un poco de un sitio y de otroy, tras probar algunos, decidirnos por uno de ellos.
• Algunos (o bastante) problemas no suelen salir a la primera y puede ser frustante pensar que, aunque trabajemos y nos esforcemos al maximos, no obtengamos resultados. Aparentemente no hemos avansado nas, pero no es tiempo perdido (en contra de lo que podamos creer) , pues nuestro inconsciente sigue trabajando sin darnos cuenta y algunas veces resulta que, cuando menos lo esperamos, sin pensar en el problema se nos aparece la solución como de una forma mágica.

14 Trazar el arco capaz con un ángulo de un segmento AB.

Por arco capaz de un segmento y un ángulo se entiende el lugar geomético (l.g.) de los puntos del plano desde los que se ve dicho segmento bajo un ángulo . Este l.g. circunferencia (P5).

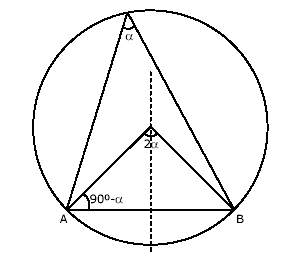
Para porder dibujar esta circunferencia se tiene en cuenta el hecho de que el ángulo central vale el doble que el inscrito.Así, dibujaremos una circunferencia cuyo centro esté en la mediatriz del segmento y tal que el ángulo que abarque sea 2 (se tendrá que dibujar en A un ángulo que valga 90º - ¿por qué?).

Habra que decidir cual de los arcos es que nos interesa. ¿Cúanto vale el ángulo del otro arco capaz?

15 Trazar la tangentes interiores a dos circunferencias exteriores.

Se puede empezar dibujando dos circunferencias exteriores (con distinto radio para que no perder generalidad) y trazar de manera aproximada una de las soluciones. Ahora se trata de ver que condiciones cumple la tangente, lo mas fácil es dibujar los radios a los puntos de contacto P y Q (que seran perpendiculares a aquella por P7). Como estos puntos no los conocemos, necesitamos ver como construirlos considerando algunos elementos que pueden estar o no presentes.

Aunque se piense que el problema es difícil y que no vamos a saberlo resolver, muchas veces disponemos de mas informacion de la que nos imaginamos y puede funcionar muy bien nuestra experiencia en casos parecidos, tengan o no los mismos elementos.

¿Podríamos trazar una paralela a la tangente por uno de los centros? ¿Qué tal si alargamos el otro radio hasta intersectar con este segmento? ¿El ángulo que forman es de 90º? ¿No se podria considerar este segmento como la tangente desde el centro a otra circunferencia? ¿Qué radio tendría esta última?...

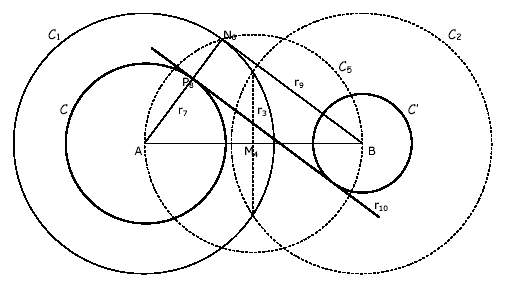
Tras este análisis el problema se transforma y pasa a ser "sencillo" cuando se ha comprendido a fondo el problema, viene ahora la sísntesis en la que se explicita el proceso directo y no el inverso de la construcción: Debemos trazar una circunferencia con centro en uno de los dos centros y de radio la suma de los radios; a continuación la tangente (por 12) desde el segundo centro a esta nueva circunferencia; el radio en el punto de contacto cortará la primera circunferencia en un punto desde el que trazaremos la perpendicular a este radio.