Polígonos regulares

Construccion de Polígonos regulares inscritos en una circunferencia

Dibujar un polígono regular de n lados y lado a es una tarea bastante sencilla. En promer lugar se averigua el ángulo interior del polígono (180º-360º/n), se traza el lado contiguo y a partir de sus mediatrices, el centro de la circunferencia circunscrita. Luego con la ayuda del compás, se determina el resto de los vértices.

Un problema mas complicado es el inverso, es decir, dada un circunferencia de radio r, determinar un polígono inscrito con un número determinado de lados. Este problema se resolvio en algunos casos y dio origen a investigaciones diversasa muy ricas, desde su utilizacion para el calculo de por parte de Arquímides a ser uno de los motivos que permitieron la resolucion de vario problemas clásicos en el siglo XIX.

Nota: en la seccion de descargas se especifican alguna de estas construcciones.

Veamos algunos ejemplos sencillos.

1 Dibujar un héxagono en una circunferencia de radio 5 cm.

El triángulo cuyos vértices son el centro de la circunferencia y dos vértices consecutivos del hexágono forman un triángulo equilátero (es isóceles y el ángulo central es de 60º), por lo que el lado del hexágono es igual al radio de la circunferencia. Así bastará marcar con el compás los vértices del hexágono con la misma abertura con la que se ha trazado la circunferencia.

2 Dibujar un cuadrado inscrito en una circunferencia de radio 5 cm

A partir del centro e la circunferencia se traza un diámetro y luego, la mediatriz de este.

3 dibujar un pentágono inscrito en una circunferencia de radio 5 cm.

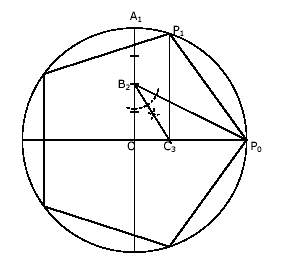
Si O es el centro de la circunferencia y P0, A1 los extremoos de los diámetros horizontal y vertical respectivamente, por 1 determinamos B2 punto medio del segmento OA1 y C3 como punto de interseccion de OP0 con la bisectrizdel ángulo OB2P0. Levantandopor C3 una vertical encontramos la circunferencia en el punto P1 que sera el segundo vértice del pentágono. El resto de los vértices los obtendremos trazando arcos con el compás con una abertura igual a P0P1.

4 Método general para contruir polígonos regulares de n lados.

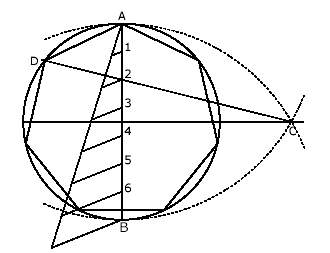
Utilizaremos como ayuda la conruccion del heptágono. Dada una circunferencia, consideramos el diámetro vertical AB y lo dividimos en 7 partes (Se utiliza P2 dibujando segmentos unitarios sobre una semirecta auxiliar y oblicua que parte de A). Por otra parte, sea C un segmento que pasa por la división 2 anterior, el punto D de corte de este segmento con la circunferencia original es el segundo vértice del héptagono (el primero es A), los demas los determinamos ayudándolos con el compás con la abertura AD.

Desgraciadamente, este procedimiento funciona mientr no necesitemos dibujos o valores más aproximados, pues el método no es exacto. Legados a este punto podríamos preguntarnos si la construcción del pentágono es exacto solo lo parece. La respuesta es que el procedimiento es exacto.

El problema general de la construccion de polígonos regulares es na circunferencia siguio abierto hasta el siglo XIX. En realidad fue Gauss quien, a los 18 años, resolvio la construccion del polígono de 17 lados y sentó las bases para la resolucion gloval del problema.

Nota: la construcción del poligono de 5 lados y la construccion general se encuentran en la seccion de descargas para que lo puedan ver en el CABRI