Ejercicios 4

Listado de ejercicios Nº4

Grafos y Algoritmos
Bienvenidos a Grafos y Algoritmos

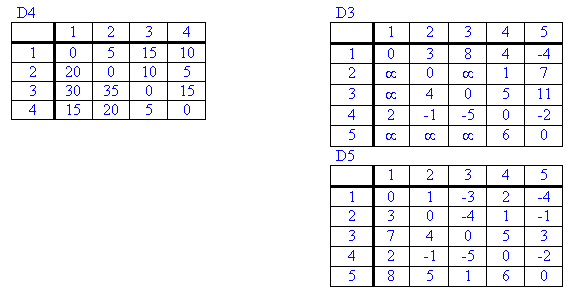
PARA LOS SIGUIENTES DIGRAFOS, DETERMINE LA RUTA DE COSTO MÍNIMO, UTILIZANDO EL ALGORITMO DE FLOYD :

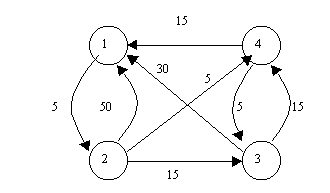
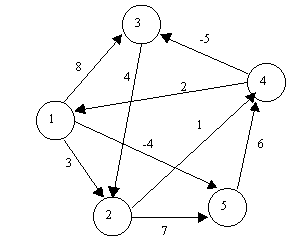
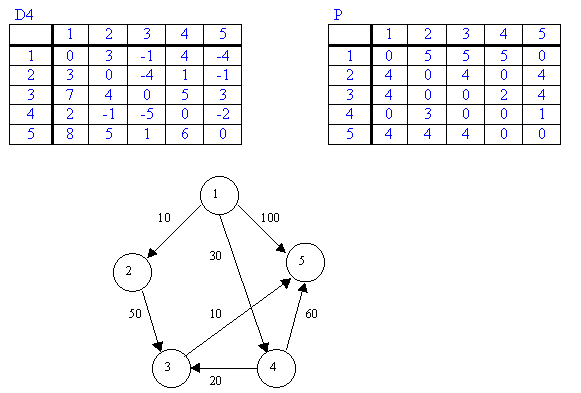
PARA EL SIGUIENTE DIGRAFO, DETERMINE LA RUTA DE COSTO MÍNIMO, UTILIZANDO EL ALGORITMO DE DIJKSTRA:

Iter	S	W	D[2]	D[3]	D[4]	D[5]	P
1	{1}	-	10	µ	30	10	(0,1,0,1,1)
	{1,2}	2	10	60	30	10	(0,1,2,1,1)
	{1,2,4}	4	10	50	30	90	(0,1,4,1,4)
	{1,2,4,3	3	10	50	30	60	(0,1,4,1,3)
	{1,2,4,3,5}	5	10	50	30	60	(0,1,4,1,3)

P=(0,1,4,1,3)

ENCONTRAR EL ORDEN DE LAS SIGUIENTES FUNCIONES

t(n) = 27n²+355/113n +12

t(n) = 27n²+355/113n +12 ; n² m n " n m 1

n² m 1 " n m 1

t(n) [ 27n²+355/113n²+12n²

t(n) [ 42 16/113 n²

t(n) c O(n²)

por que $ c=42 16/113, $ n₀=1 / t(n) [ cn² " n m n₀

t(n) = 1/1000 n³

¿t(n) c O(n²)?

$ c c R⁺; $ n₀ c N⁺

1/100 n³ [ c n²; " n m n₀

1/100 n³ [ c n²

n [ 1000c

por contradicción: 1/1000 n³ v O(n²)

f(n) = n³/1000 - 100n² – 100n +3

f(n) = n³/1000 - 100n² – 100n +3 ; n³ ³ n² " n ³ 1

n³ ³ n " n ³ 1

n³ ³ 1 " n ³ 1

f(n) = n³/1000 - 100n³ – 100n³+3n³

f(n) = -196,999n³ ; $ c=-196,999; $ n₀ = 1 /

f(n) £ cn³ è f(n) Î O(n³)

f(n,m) = 43n² – 28m

g(n) = 43n², g(n) Î O(n²)

t(m) = -28m , t(m) Î O(m)

Por regla del Máximo.

f(n,m) Î O(máx{n²,m})

è f(n,m) Î O(n²)

CUÁL DE LAS SIGUIENTES AFIRMACIONES SON CORRECTAS,JUSTIFIQUE.

1. 10n² Î O(n³) V

10 n² [ c n³; " n m n₀

c=10

10 n² [ 10 n³; " n m 1

è $ c=10 ; $ n₀ = 1 /

10 n² [ c n³; " n m n₀

10 n² c O(n³ )

n² Î W (n³) F

" n³ 1, n²£ dn³ , d Î R⁺ è n² Ï W (n³)

2ⁿ Î Q (2ⁿ⁺¹) V

lim 2ⁿ = lim 2^n-(n+1) = lim 2 =2 è 2ⁿ Î Q (2ⁿ⁺¹)

nè µ 2^{n+1 n}è µ nè µ

n! Î Q ((n+1)!) F

lim n! = lim n! = lim 1 = 0 è n! Ï Q ((n+1)!)

nè µ (n+1)! ⁿè µ (n+1) n! ⁿè µ (n+1)

10n² + 5n Î O(nlog₂n) F

lím nlog₂n = lim log₂n = lim ln n por L’H

nè } 10n² + 5n ⁿè } 10n+5 ⁿè } ln2(10n+5)

lím 1/n = lim 1 = 0

nè } 10 ln2 ⁿè } 10ln2

è (nlog₂n) Î O(10n² + 5n)

6.- å i^k Î O(n^k+1) V

ⁱ⁼¹

å i^k = 1^k+2^k+3^k+4^k+...n^k

ⁱ⁼¹£ n^k+n^k+...n^k

= n*n^k=n^k+1

è _n

å i^k £ c n^k+1

ⁱ⁼¹

è _n

å i^k Î O(n^k+1)

ⁱ⁼¹

ORDENAR LAS SIGUIENTES FUNCIONES UTILIZANDO LOS SIGNOS Ì O =.

1/1000n³, n²

lím n² = lim 1000 = 0

nè } n³/1000 nè } n

è O(n²) Ì O(n³/1000)

2. 4ⁿ ; n!

4ⁿ £ c n! , " n ³ 1

O(4ⁿ) Í O(n!)

C=?

tenemos O((n-1)!) Ì O(n!)

4ⁿ; (n-1)!

4ⁿ = 4*4*4*4*4*4*4*.....*4

4ⁿ£ 4*4*4*4*4*5*6*7*8*... (n-1)

4ⁿ£ 4⁴*1*2*3*4*5*6*7*......(n-1)

4ⁿ£ 4⁴*(n-1)!

è 4ⁿ£ 4⁴(n-1)!

$ c=4⁴, $ n₀ =1è 4ⁿ£ c(n-1) / " n ³ n₀

O(4ⁿ) Í O((n-1)!)

Como O((n-1)!) Ì O(n!)

O(4ⁿ) Ì O(n!)

(2n)²; (n+1)!; 2ⁿ; 2²ⁿ; n!; 2ⁿlogn; 2ⁿ⁺¹; (n+1)²; n²

a).- O(n2) Ì O(2n)

lim n² . por L’H

nè µ 2ⁿ

lim 2n = lim 2 = 0

nè µ 2ⁿln2ⁿè µ 2ⁿ(ln2)²

b).- O((2n)²) = O(n²)

c).- O((n+1)²) = O(n²)

d).- O(2ⁿ) =O(2ⁿ⁺¹)

e).- lim 2ⁿ = lim 1 = 0 è O(2ⁿ) Ì O(2²ⁿ)

nè µ 2^{2n n}è µ 2ⁿ

f).- O(2ⁿ) ^v/s O(n!)

n! = 1*2*3*4*5*6...*n

n! ³ 1*2*3*4*4*4....*4

n! = 6*4^n-3

n! ³ 6/4³*4ⁿ è 4ⁿ£ 4³/6*n!

c=4³/6 , $ n=1 / 4ⁿ £ c n!

è (4ⁿ)Î n! è O(2²ⁿ) Ì O(n!)

g).- n! ^v/s (n+1)!

lim (n+1)! = lim (n+1) n! = µ

nè µ n!ⁿè µ n!

è O(n!) Ì O((n+1)!)

Finalmente:

O((2n)²) = O((n+1)²) = O(n²) Ì O(2ⁿ) = O(2ⁿ⁺¹) Ì O(2²ⁿ) Ì O(n!) Ì O((n+1)!

4.- n³; 2ⁿ, nlogn, logn , 1, n, n²

a).- lim n = lim 1 = 0 è O(n) Ì O(n²)

nè µ n^{2 n}è µ n

b).- lim n² = lim 1 = 0 è O(n²) Ì O(n³)

nè µ n^{3 n}è µ n

c).- lim n³ = lim 3n² = lim 6n = lim 6 = 0

nè µ 2^{n n}è µ 2ⁿln2ⁿè µ 2ⁿ(ln2)^{2 n}è µ 2ⁿ(ln2)³

O(n³) Ì O(2ⁿ)

d).- lim log n = lim 1 = 0 è O(log n) Ì O(n log n)

nè µ nlogn ⁿè µ n

e).- lim log n = lim 1/n = 0 è O(log n) Ì O(n)

nè µ n ⁿè µ ln10*n

f).- lim 1 = 0 è O(1) Ì O(log n)

nè µ logn

g).- lim n log n = µ è O(n) Ì O(n log n)

nè µ n

h).- lim nlog n = lim 1/n = 0 è O(nlog n) Ì O(n²)

nè µ n² ⁿè µ ln10

Finalmente:

O(1) Ì O(logn) Ì O(n) Ì O(nlogn) Ì O(n²) Ì O(n³) Ì (2ⁿ)

RECURRENCIA

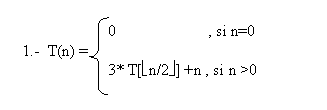
n

Desarrollo T(n)

0

0

1

3*0+1

2

3*1+2

4

3*(3+2)+4

8

3*(3*(3+2)+4)+8

2^k

3^k+ 3^k-1* 2 + 3^k-2* 2²+ 3¹* 2^k-1+ 2^k

è å 3^k-i 2ⁱ

è å 3^k 3^-i 2ⁱ

è 3^k å (2/3)ⁱ

è 3^k[(1-(2/3)^k+1)/(1-(2/3))

è 3^k+1 (1-(2/3)^k+1)

è 3^k+1 – 2^k+1

è T(2^k)= 3^k+1 – 2^k+1

è T(n)=?

n= 2^k

k=log₂n

T(n)= 3 ^log₂ⁿ⁺¹ – 2 ^log₂ⁿ⁺¹

T(n)= 3*3 ^log₂ⁿ – 2*2 ^log₂ⁿ

T(n)= 3*n ^log₂³- 2n; " n potencia de 2

T(n) Î O(n ^log₂³ /n es potencia de 2)

è T(n) es creciente

è n ^log₂³ es lisa

è T(n) Î Q (n ^log₂³) (" n)

RECURRENCIA HOMOGENIA

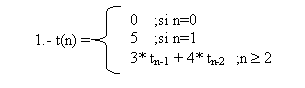
t_n – 3* t_n-1 – 4* t_n-2 =0 k=2, a₀=1, a₁ =-3, a₂=-4

X² – 3X – 4 = 0

(X-4)(X+1) =0

X₁=4 X₂=-1

f(n) = C₁*4ⁿ + C₂ * (-1)ⁿ; " n ³ 2

f(0) = 0 = C₁ + C₂è C₁= -C₂

f(1) = 5 = 4 C₁ + C₁

C₁=1 è C₂ = -1

è f(n) = 4ⁿ- (-1)ⁿ ; n ³ 0

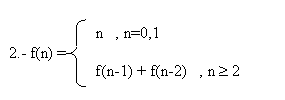
Recurrencia: t(n)-t(n-1)-t(n-2) = 0

Polinomio característico: a₀ = 1, a₁ = -1, a₂ = -1, K =2

X² – X – 1 = 0

X = 1 ± Ö 5 è X₁= 1 + Ö 5 y X₂ = 1 - Ö 5

2 2 2

è f(n) = C₁ (1+Ö 5)ⁿ + C₂ (1-Ö 5)ⁿ n ³ 2

2ⁿ2ⁿ

f(0) = 0 = C₁ + C₂ è C₁ =- C₂

f(1) = 1 = C₁ (1+Ö 5) + C₂ (1-Ö 5) = C₁Ö 5

C₁ = 1/Ö 5 è C₂ = -1/Ö 5

è f(n) = (1+Ö 5)ⁿ - (1-Ö 5)ⁿ n ³ 0

2ⁿÖ 5 2ⁿÖ 5

RECURENCIA HOMOGENIA CON RAICES MULTIPLES

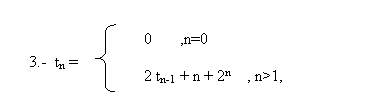
Polinomio característico: (K=3)

X³ – 5X² + 8X – 4 = 0

(X-1)(X-2)² = 0 è X₁=1 , X₂ =2

t(n) = C₁*1ⁿ+ C₂*2ⁿ + C₃n 2ⁿn >2

n=0 0 = C₁ + C₂ + C₃, C₁ = -2

n=1 1 = C₁ + 2C₂ + 2 C₃ , C₂ = 2

n=2 2 = C₁ + 4C₂ + 8 C₃ , C₃ = -1/2

è t(n) = -2 + 2ⁿ⁺¹ – n2^n-1 ,n ³ 0

RECURRENCIA NO HOMOGENIA.

1.- t_n = 2 t _n-1 + 3ⁿ

polinomio è (X-2)(X-3) = 0

t(n) = C₁2ⁿ + C₂3ⁿ

2.- t_n = 2 t_n-1 + n

polinomio è (X-2)(X-1)² = 0

t(n) = C₁2ⁿ + C₂1ⁿ + C₃1ⁿ

polinomio è (X-2)²(X-1)² = 0

t(n) = C₁ + C₂n + C₃2ⁿ + C₄n2ⁿ

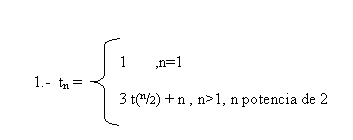
TECNICA DEL CAMBIO DE VARIABLE.

t(n) = 3 t(ⁿ/2) + n , n = 2ⁱ , 1=1,2,...

t(2ⁱ) = 3 t(2ⁱ/2) + 2ⁱ = 3 t (2^i-1) + 2ⁱ

t(i) = t(2ⁱ) è t_i = 3 t_i-1 + 2ⁱ

t(2^i-1) = t_i-1

polinomio característico è (X-3)(X-2)

t(i) = C₁3ⁱ + C₂2ⁱ , como n = 2ⁱ, i = log₂n

t(log₂n) = t(2^log₂ⁿ) = t(n)

t(log₂n) = t(n) = C₁3^log₂ⁿ + C₂2^log₂ⁿ

t(n) = C₁n^log₂³ + C₂n

t(n) Î Q (n^log₂³) " n que sea potencia de 2

como t_n es creciente y n^log₂³ es lisa

t(n) Î Q (n^log₂³) " n

n	Desarrollo T(n)
0	0
1	3*0+1
2	3*1+2
4	3*(3+2)+4
8	3(3(3+2)+4)+8
2^k	3^k+ 3^k-1* 2 + 3^k-2* 2²+ 3¹* 2^k-1+ 2^k