Listado de Ejercicios Nº3

de Grafos Y Algoritmos

Bienvenidos a Grafos y Algoritmos

 

Responder cada pregunta (10 Puntos cada una), con V(verdadero) o F(falso). Si es F entonces justificar en una líneas.

 

    1. Sea el grafo: G = (V, A) con n vértices y sin ciclos. Si el grado (x) + grado (y) ³ n-1 para x ¹ y entonces G no tiene camino Hamiltoneano.

      2. F ,Si no tiene ciclos es un arbol, y no todos los arboles tienen ciclo Hamiltoniano

    2. Sea el grafo: G = (V, A), entonces G tiene un ciclo Euleriano si grado (v) ³ 2, v Î V.

      3. F, el problema de los puentes es de grado >=2 y no tiene ciclo Euleriano

    3. Sea el grafo: G = (V, A) y a Î V con grado (a) > 2, entonces las dos aristas incidentes con el vértice a deben aparecer en cualquier ciclo Euleriano.

      4. V

    4. Todo grafo completo no tiene camino Hamiltoneana.

      5. F, todos lo tienen

    5. Todo grafo completo (con n ³ 2 ) tiene ciclo Hamiltoneano.

      6. F,no se puede volver al vértice de partida, tiene solo camino Hamiltoniano

    6. Un grafo bipartito Gm,n es Hamiltoneano si y solo si m = n

      7. F

    7. Sea G un grafo con n vértices y con n mayor o igual a 2 y con el grado de cada vértice siendo mayor o igual a n/2, entonces G es un grafo Hamiltoneano.

      8. V

    8. El siguiente grafo no es planar. F

      9.  

    9. El siguiente grafo es un grafo 3-conexo V

      10.  

    10. El siguiente grafo tiene ciclo Hamiltoneano pero no camino Hamiltoneano.

 

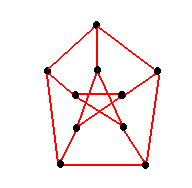
 F, es al revés tiene camino pero no tiene ciclo ya que si se parte desde el vértice de más arriba no se puede volver a este

 

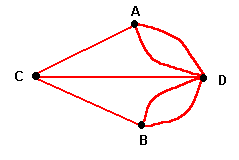
k) El siguiente grafo no corresponde al grafo de "EULER".

F
Bienvenidos a Grafos y Algoritmos
 
Menú Principal