CONONCIENDO LA DISTRIBUCION NORMAL
Una de las distribuciones más importantes, cuando se quiere describir una variable
aleatoria continua
es la distribución normal, ya que tiene muchas aplicaciones en variados contextos;
por ejemplo, la estatura y la masa de las personas, mediciones
científicas, precipitaciones, puntajes de pruebas, entre muchas otras.
En este caso, decimos que la variable aleatoria X tiene distribución normal con media
μ y desviación estándar σ, y la denotamos como X ~ N(μ, σ).
Esta distribucion tiene las siguientes caracteristicas:
1. La variable puede tomar cualquier valor: (-∞, +∞)
2. La función de densidad, es la expresión en términos de ecuación matemática de la curva de Gauss:
Para calcular distintas probabilidades con esta distribucion, se define la siguiente funcion de densidad

Desde el punto de vista de la grafica tiene lo siguiente
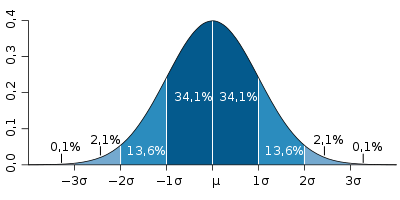
la cual posee varias caracteristicas
en primer lugar la grafica es simetrica con respecto al eje Y (tal como se puede ver con los porcentajes)
Para la distribución normal se cumple que:
• El 68,26 % de los valores de una variable aleatoria normal está
dentro de más o menos una desviación estándar de su media.
• El 95,45 % de los valores de una variable aleatoria normal está
dentro de más o menos dos desviaciones estándar de su media.
• El 99,73 % de los valores de una variable aleatoria normal está
dentro de más o menos tres desviaciones estándar de su media.
La gráfica de una distribución normal es una curva en forma de campana, que es simétrica respecto
de la media. El área bajo esta curva es 1.
Sin embargo, realizar ejercicios usando directamente la distribucion normal, es algo complejo para ello tenemos lo siguiente:
Si tenemos una variable aleatoria continua con distribución normal, en la que la
media es igual a 0 y la desviación estándar igual a 1,
es decir, μ = 0 y σ = 1,entonces la
variable aleatoria tiene distribución normal estándar y se denota X ~ N(0, 1).
Para el cálculo de probabilidades en distribución normal estándar se han construido
tablas que presentan las áreas bajo las curvas y, por lo tanto, permiten determinar de
manera rápida las probabilidades de que el valor de una variable aleatoria se encuentre
en un intervalo.
Para calculos se utiliza una tabla que permite determinar la probabilidad
de que una variable aleatoria con distribución normal estándar sea menor que
un valor dado z, es decir, P(X < z).
A continuacion se presenta un video el cual muestra como realizar ejercicios con esta distribucion
pincha aqui
A continuacion es tu turno para desarrollar las actividades,
el link siguiente te llevara a los ejercicios correspondientes a este tema
en nuestra proxima clase, veremos como esta distribucion normal estandar, nos ayudara a realizar los calculos dificiles
que se presentan en cualquier tipo de distribucion normal


