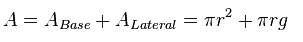Geometría Sólida

Es la rama de la geometría que se encarga del estudio de las figuras geométricas voluminosas que ocupan un lugar en el espacio; estudia las propiedades y medidas de las figuras geométricas en el espacio tridimensional o espacio euclídeo.

Estos cuerpos pueden ser de dos clases: Poliedros y No poliedros.

POLIEDROS
Sólidos Platónicos		Los sólidos platónicos o regulares son poliedros convexos tal que todas sus caras son polígonos regulares iguales entre sí, y en que todos los ángulos sólidos son iguales.
Tetraedro	Hexaedro	Octaedro	Dodecaedro
Prisma		Un prisma es un poliedro con una base poligonal de n lados, una copia de traslación (no en el mismo plano que la primera), y otras n caras (todas necesariamente deben ser paralelogramos) que une los lados correspondientes de las dos bases.
Prisma Triangular	Prisma Cuadrangular	Prisma Pentagonal	Prisma Hexagonal
Pirámide		Una pirámide es un poliedro limitado por una base, que es un polígono (la cara inferior) y por varias caras laterales, que son triángulos con vértices coincidentes en un punto denominado ápice.
Piramide Triangular	Piramide Cuadrangular	Piramide Pentagonal	Piramide Hexagonal

NO POLIEDROS
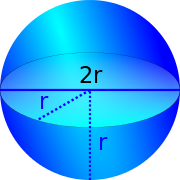
Esfera		Una superficie esférica es una superficie de revolución formada por el conjunto de los puntos del espacio (de tres dimensiones) cuyos puntos equidistan de otro punto llamado centro. La esfera, como superficie de revolución, se genera haciendo girar una superficie semicircular alrededor de su diámetro.
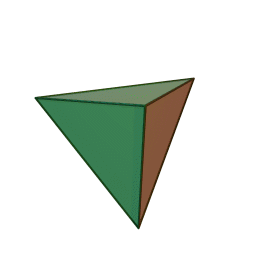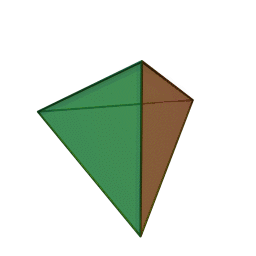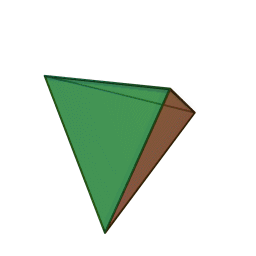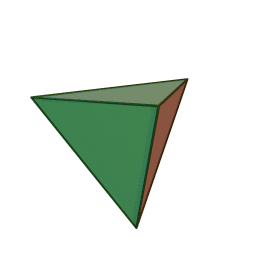
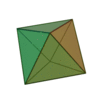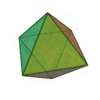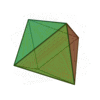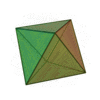
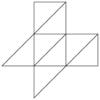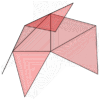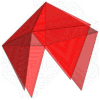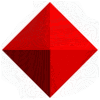
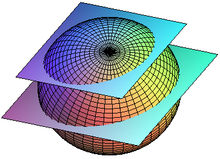
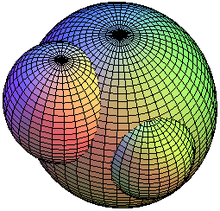
Tetraedro	Sección de una esfera por un plano	Intersección de esferas	Plano tangente a una esfera
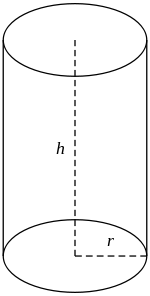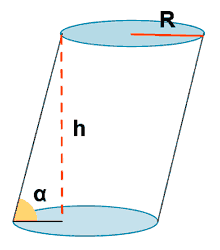
Cilindro		En geometría, un cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, denominada directriz del cilindro.
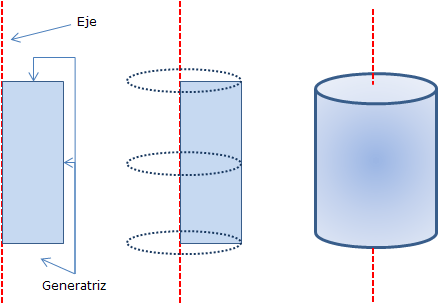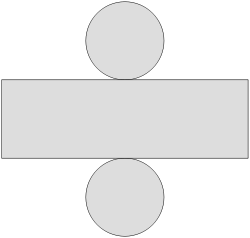
Volumen= Area=	Cilindro Oblicuo	Cilindro de revolución	Superficie cilindrica
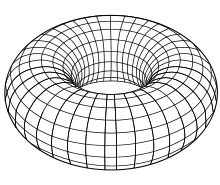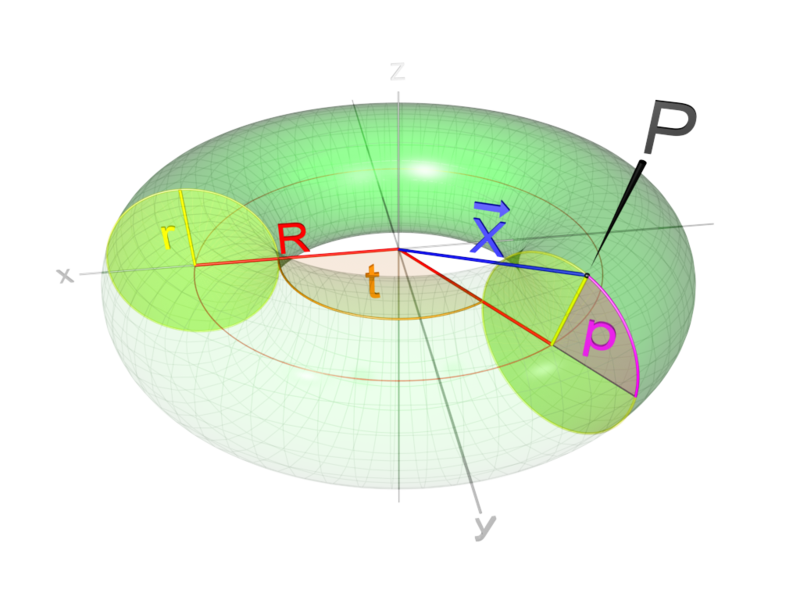
Toro		En geometría, un toro es una superficie de revolución generada por una circunferencia que gira alrededor de una recta exterior coplanaria (en su plano y que no la corta) o, llanamente, la curva tridimensional que resulta de hacer girar una circunferencia alrededor de un eje que no la corta.
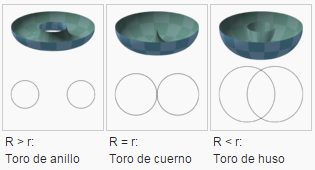
Intersección toro y plano	Toro cortado por un plano	Toro con sus principales variables	Clases de toro
Cono	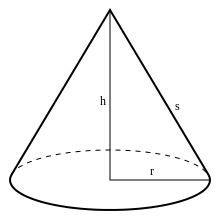	En geometría, un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos. Al círculo conformado por el otro cateto se denomina base y al punto donde confluyen las generatrices se llama vértice o cúspide.
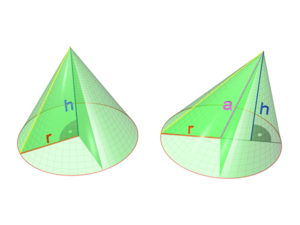
Secciones cónicas	Sección de un cono recto y un cono oblicuo	Superficie cónica	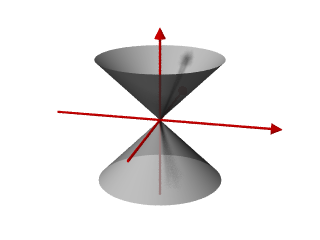Área del Cono:
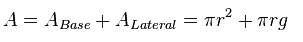