Superficies cuadráticas www.udec.cl/~juanerodriguez
Las secciones cónicas: elipse, parábola e hipérbola tienen su generalización al espacio tridimensional en elipsoide, paraboloide e hiperboloide.
|
|
Definición (superficies cuadráticas) |
|
|
La gráfica de una ecuación de segundo grado en tres variables
se conocen como superficies cuadráticas, salvo casos degenerados.
|
Observación: en la ecuación de segundo grado
![]() deliberadamente no hemos incluido los
términos mixtos
deliberadamente no hemos incluido los
términos mixtos ![]() ,
, ![]() y
y ![]() ,
pues la presencia de estos genera superficies con rotación, tema que no
trataremos en el curso
,
pues la presencia de estos genera superficies con rotación, tema que no
trataremos en el curso
![]() Elipsoide
Elipsoide
La gráfica de la ecuación:
![]()
corresponde a un elipsoide. Es simétrico con respecto a cada uno de los tres
planos coordenados y tiene intersección con los ejes coordenados en ![]() ),
),
![]() y
y
![]() .La
traza del elipsoide sobre cada uno de los planos coordenados es un único punto
(! ) o una elipse. La figura 1 muestra su gráfica.
.La
traza del elipsoide sobre cada uno de los planos coordenados es un único punto
(! ) o una elipse. La figura 1 muestra su gráfica.
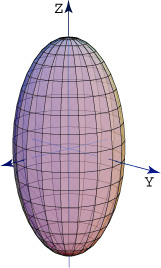
Figura 1. Elipsoide
![]() Paraboloide elíptico
Paraboloide elíptico
La gráfica de la ecuación
![]()
es un paraboloide elíptico. Sus trazas sobre
planos horizontales ![]() son
elipse :
son
elipse :
![]()
Sus trazas sobre planos verticales, ya sean ![]() o
o
![]() son
parábola.
son
parábola.
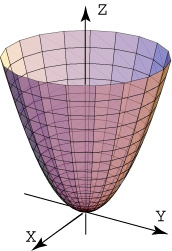
Figura 2. Paraboloide elíptico
![]() Paraboloide hiperbólico
Paraboloide hiperbólico
La gráfica de la ecuación:
![]()
es un paraboloide hiperbólico. Sus trazas sobre planos horizontales![]() son hipérbolas o dos rectas (
son hipérbolas o dos rectas (![]() ).
Sus trazas sobre planos verticales paralelos al plano
).
Sus trazas sobre planos verticales paralelos al plano ![]() son
parábolas que abren hacia abajo, mientras que las trazas sobre planos
verticales paralelos al plano
son
parábolas que abren hacia abajo, mientras que las trazas sobre planos
verticales paralelos al plano ![]() son
parábolas que abren hacia arriba. Su gráfica tiene la forma de una silla de
montar, como se observa en la figura 3. www.udec.cl/~juanerodriguez
son
parábolas que abren hacia arriba. Su gráfica tiene la forma de una silla de
montar, como se observa en la figura 3. www.udec.cl/~juanerodriguez
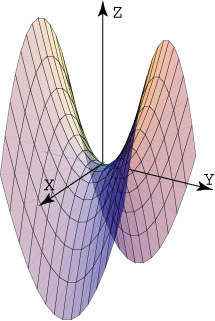
Figura 3. Paraboloide hiperbólico
![]() Cono elíptico
Cono elíptico
La gráfica de la ecuación:
![]()
es un cono elíptico. Sus trazas sobre planos horizontales ![]() son
elipses. Sus trazas sobre planos verticales corresponden a hipérbolas o un par
de rectas. Su gráfica se muestra en la figura 4.
son
elipses. Sus trazas sobre planos verticales corresponden a hipérbolas o un par
de rectas. Su gráfica se muestra en la figura 4.
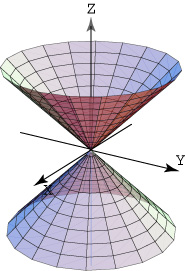
Figura 4. Cono elíptico
![]() Hiperboloide de una hoja
Hiperboloide de una hoja
La gráfica de la ecuación:
![]()
es un hiperboloide de una hoja.Sus trazas sobre planos horizontales ![]() son
elipses
son
elipses
![]()
Sus trazas sobre planos verticales son hipérbolas o un par de rectas que se intersecan (!). Su gráfica se muestra en la figura 5.
.
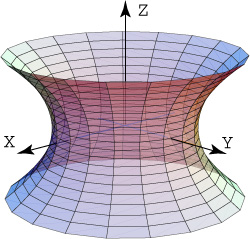
Figura 5. Hiperboloide de una hoja
![]() Hiperboloide de dos hojas
Hiperboloide de dos hojas
La gráfica de la ecuación:
![]()
es un hiperboloide de dos hojas. Su gráfica consta de dos hojas separadas. Sus
trazas sobre planos horizontales ![]() son
elipses y sobre planos verticales son hipérbolas (figura 6).
son
elipses y sobre planos verticales son hipérbolas (figura 6).
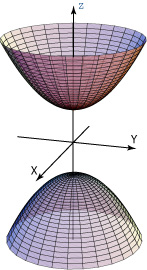
Figura 6. Hiperboloide de dos hojas
Ejemplo 1
Identifique cada una de las siguientes superficies cuadráticas:
a.) ![]()
b.) ![]()
Solución
a.) Dividiendo por 4 la primera ecuación obtenemos:
![]()
lo cual corresponde a un hiperboloide de dos hoja, con el eje ![]() como
eje de simetría.
como
eje de simetría.
b.) Completando el cuadrado en ![]() para
la segunda superficie obtenemos:
para
la segunda superficie obtenemos:
![]()
que corresponde a un paraboloide elíptico con eje paralelo al eje ![]() . www.udec.cl/~juanerodriguez
. www.udec.cl/~juanerodriguez