CÁLCULO NUMÉRICO (521230)

LABORATORIO 7 - 2017-2

Ecuaciones Diferenciales Ordinarias: Problemas de Valores Iniciales

Contents

EJERCICIO 1

1.1 Resuelva el problema de valores iniciales (P.V.I.) con ode45 suponiendo N = 3000, E(0) = 150, m = 1.8 y c = 0.001. Llame antes a odeset para hacer AbsTol igual a 1e-8 y RelTol igual a 1e-4.

clc;clear;close all
options=odeset('RelTol',1e-4,'AbsTol',1e-8);

N_t = 3000; %total de personas
E_0 = 150; %enfermos iniciales
M_0 = 0; %muertos iniciales
S_0 = N_t - E_0 - M_0; %sanos iniciales (aquellos no enfermos y no muertos)

m = 1.8;
c = 0.001;

f=@(t,M) m.*(N_t - S_0.*exp(-c.*M/m) - M);
[t,M] = ode45(f,[0 10],M_0,options);

1.2 Dibuje, en un mismo gráfico, el número de personas sanas, muertas y enfermas en el período considerado (de 10 semanas).

E = N_t - S_0*exp(-(c/m)*M) - M;
S = S_0*exp(-(c/m)*M);
plot(t,M,'k',t,E,'g',t,S,'b');
grid on
legend('Muertas','Enfermas','Sanas');

1.3 ¿Al cabo de cuántas semanas aproximadamente se mantiene casi constante el número de personas sanas, enfermas y muertas en el grupo considerado?

Esta parte se puede hacer mirando el gráfico y mediante el cuadriculado, estimar el momento "t" donde se vuelve constante. O llamando los vectores y notando dónde se hace constante. Una manera más o menos extraña de conseguirlo también, es la siguiente:

in = find(t > 5,1); %sabemos que los muertos no son constantes antes de la semana 5 al menos,
%así que buscamos el primer valor de t que sea mayor a 5
mu = abs(M(in:end-1) - M(in+1:end)); %este es un vector que compara los muertos entre intervalos de t
%y entrega el valor absoluto. Es decir verifica cuántos mueren entre
%semanas.
ap = find(mu < 0.5,1); %digamos que se mantiene constante cuando muere menos de "media persona" por primera vez
cte = t(in + ap); %ubicamos la semana en que sucede esto
sem = round(cte); %la función round redondea el valor a un entero.
fprintf('Los muertos (y por consiguiente, enfermos y sanos) se mantienen constantes aproximadamente a partir de la semana %i',sem);

Los muertos (y por consiguiente, enfermos y sanos) se mantienen constantes aproximadamente a partir de la semana 9

1.4 ¿Cuál es el número de personas que ha muerto a causa de la enfermedad 8 semanas después de comenzada la epidemia?

[t8,M8] = ode45(f,[0 8 10],M_0,options);
fprintf(1,'Al cabo de 8 semanas han muerto aprox. %f personas\n',M8(2));

Al cabo de 8 semanas han muerto aprox. 2118.600359 personas

EJERCICIO 2

2.1 Cuando 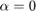$\alpha = 0$, conejos y zorros no interactúan. Resuelva la ecuación diferencial a lo largo de un año en el caso en que inicialmente hay 100 animales de cada especie. Compruebe que en tal caso los conejos hacen lo que mejor saben hacer, mientras los zorros se van muriendo de hambre.

clc;clear;close all
F = @(t,y,a)[2*y(1)-a*y(1)*y(2);
    -y(2)+a*y(1)*y(2)]; %aquí la función depende de un parámetro "a"

y_0 = [100;100];
f = @(t,y)F(t,y,0); %aquí generamos una función "hija" que es idéntica a F, pero con a = 0 fijo
[t,y] = ode45(f,[0 1],y_0);
c = y(:,1);
z = y(:,2);

figure
hold on
plot(t,c,'b');
plot(t,z,'r');
hold off
legend('Conejos','Zorros');
grid on

2.2 Calcule la evolución de ambas poblaciones a lo largo de 12 años en el caso en que la constante de interacción es 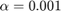$\alpha = 0.001$ y que la población inicial es de 300 conejos y 150 zorros. ¿Qué conclusión puede extraer en este caso?

y_0 = [300;150];
[t,y] = ode45(@(t,y)F(t,y,0.01),[0 12],y_0); %podemos saltarnos la línea de generar la función "hija"
%y escribir @(t,y)F(t,y,0.01) directamente como argumento de ode45
c = y(:,1);
z = y(:,2);

figure
hold on
plot(t,c,'b');
plot(t,z,'r');
hold off
legend('Conejos','Zorros');
grid on

2.3 Repita la simulación anterior pero con poblaciones iniciales de 15 conejos y 22 zorros. ¿Cuál es ahora la conclusión?

y_0 = [15;22];
[t,y] = ode45(@(t,y)F(t,y,0.01),[0 12],y_0);
c = y(:,1);
z = y(:,2);

figure
hold on
plot(t,c,'b');
plot(t,z,'r');
hold off
legend('Conejos','Zorros');
grid on

EJERCICIO 3

3.2 Resuelva el problema de valores iniciales resultante con $t \in [0,\ 20]$ y suponiendo A = 2.5.

clc;clear;close all

F = @(t,y)[y(2);
    (y(1)^(-3*1.4) - 1 - (3/2)*y(2)^2)/y(1)];
y_0 = [2.5;0];
[t,y] = ode45(F,[0 20],y_0);

3.3 Grafique la aproximación resultante y observe que es una función periódica, ¿cuál es el período aproximado de la misma? ¿Entre qué valores oscila el radio R de la burbuja?

r = y(:,1);
R = 3e-6 * r;
plot(t,R,'r')
legend('R(t)')
grid on

Rmax = max(R);
Rmin = min(R);

RR = find(abs(R - Rmin) < 1e-8);
disp('R = ')
disp(RR)
%Observamos que R(t) alcanza su mínimo aproximadamente en su componente 308
%y 423.
per = abs(t(308) - t(423));
fprintf(1,'El período aproximado de R(t) es %f, y oscila entre %f y %f',per,Rmin,Rmax);

R = 
   307
   308
   309
   422
   423
   424

El período aproximado de R(t) es 4.732148, y oscila entre 0.000001 y 0.000008

EJERCICIO 4

4.1 Resuelva este problema con ode45 y ode15s tomando AbsTol = 1e-6 y RelTol = 1e-4. ¿En cuántos subintervalos divide ode45 el intervalo de integración $[0,\ 5]$ para resolver este problema? ¿En cuántos lo divide ode15s? Observe que ode15s necesita dividir $[0,\ 5]$ en muchos menos subintervalos que ode45, a pesar que las tolerancias con que ambos métodos calculan son las mismas. Este comportamiento es típico de problemas stiff.

clc;clear;close all

options=odeset('RelTol',1e-4,'AbsTol',1e-6);
F = @(x,y)100 - (1 - y);
y_0 = 2;

[x1,y1] = ode45(F,[0 5],y_0,options);
[x2,y2] = ode15s(F,[0 5],y_0,options);

int45 = numel(x1) - 1;
int15 = numel(x2) - 1;

fprintf(1,'ode45 divide a [0 5] en %i subintervalos\node15s divide a [0 5] en %i subintervalos',int45,int15);

ode45 divide a [0 5] en 56 subintervalos
ode15s divide a [0 5] en 37 subintervalos

4.2 Grafique los tamaños de paso generados por ambos métodos y la solución exacta a este problema 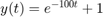$y(t) = e^{-100t} +1$.

Observe que la solución exacta de este problema varía rápidamente desde el valor inicial hasta un valor cercano a 1, pero para 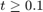$t \geq 0.1$ se mantiene casi constante. Es de esperarse que a partir ed 0.1 un método numérico para resolver este problema tome en $[0,\ 0.1]$ tamaños de paso pequeños, para poder reproducir la variación de la solución exacta, pero a partir de 0.1 usa tamaños de paso mucho mayores.

Sin embargo, en los gráficos de los tamaños de paso usados por ode45 y ode15s, sólo ode15s exhibe el comportamiento esperado. El comportamiento de ode45 es el típico de métodos no adecuados para resolver problemas stiff al usarse para resolver problemas stiff.

Y = @(t)exp(-100*t) + 1;
tpaso1 = x1(2:end) - x1(1:end-1);
tpaso2 = x2(2:end) - x2(1:end-1);

k = linspace(0,5,1000);
hold on
plot(k,Y(k),'b')
plot(x1(1:end-1),tpaso1,'r--')
plot(x2(1:end-1),tpaso2,'m--')
hold off
legend('Soluci\''on exacta','Pasos ode45','Pasos ode15s');

EJERCICIO 5

5.1 Resuelva el problema con ode45 y los pares de valores AbsTol y RelTol en la tabla 1 (indicada en el pdf) y complétela.

clc;clear;close all

F=@(x,t)-3*t.*x.^2 + 1./(1+t.^3);
x_0 = 0;

X=@(t)t./(1+t.^3);
Rt = [1e-2;1e-3;1e-4;1e-5];
At = [1e-4;1e-5;1e-6;1e-7];

for i=1:4
    options = odeset('RelTol',Rt(i),'AbsTol',At(i));
    [t,x] = ode45(F,[0 5],x_0,options);
    md(i) = max(abs(x - X(t)));
end

fprintf(1,'---------------------------------------\n');
fprintf(1,'| RelTol | AbsTol | max|x_i - x(t_i)| |\n');
fprintf(1,'|  1e-2  |  1e-4  | %17f |\n',md(1));
fprintf(1,'|  1e-3  |  1e-5  | %17f |\n',md(2));
fprintf(1,'|  1e-4  |  1e-6  | %17f |\n',md(3));
fprintf(1,'|  1e-5  |  1e-7  | %17f |\n',md(4));
fprintf(1,'---------------------------------------\n');

---------------------------------------
| RelTol | AbsTol | max|x_i - x(t_i)| |
|  1e-2  |  1e-4  |          0.145108 |
|  1e-3  |  1e-5  |          0.145394 |
|  1e-4  |  1e-6  |          0.145392 |
|  1e-5  |  1e-7  |          0.145407 |
---------------------------------------

5.2 Con los valores devueltos en el último llamado a ode45 grafique la solución exacta y los tamaños de paso con los que ha calculado ode45.

Observe que en el tramo en el que la solución exacta del problema varía más rápidamente los tamaños de paso con los que calcula ode45 son más pequeños.

figure(1)
plot(t,t./(1+t.^3))
figure(2)
plot(t(1:end-1),t(2:end)-t(1:end-1))

EJERCICIO 6

6.3 Escriba un programa tipo rutero en ambiente MATLAB que realice las siguientes tareas:

  a) Resuelva el problema utilizando el Esquema de Euler Implícito,
  considerando N = 100.
clc;clear;close all
N = 100;
h = 1.5/N;

for i=1:N+1
    t(i)=(i-1)*h; %PARTICIÓN
end
yeuler(:,1) = [0;
               2;
               0];
for i=1:N
    b = yeuler(:,i) + [h;
        0;
        h*exp(i*h)];
    %considerando t_{i+1} = i*h, también se podía usar t(i+1) directamente
    A = [ 1 - 3*h*sin(i*h),      -(2*i*h^2) , 0;
                     0,               1     , -h;
                  -2*h,              h*5    , 1-i^2*h^3];
    yeuler(:,i+1) = A\b;
end

  b) Resuelva el problema utilizando el comando |ode45|, utilizando la
  misma partición definida en el ítem anterior.
F = @(t,y)[3*sin(t).*y(1) + 2*t.*y(2) + 1;
    y(3);
    2*y(1) + t.^2.*y(3) - 5*y(2) + exp(t)];
y_0 = [0;
       2;
       0];
[t45,y45] = ode45(F,t,y_0);

  c) En una misma figura grafique x(t) obtenidos por el Método de Euler
  implícito y el comando |ode45|.
figure(1)
hold on
plot(t,yeuler(1,:),'b');
plot(t,y45(:,1),'r');
hold off
legend('Euler Impl\''icito','ode45');

  d) En otra figura grafique y(t) obtenidos por el Método de Euler
  implícito y el comando |ode45|.
figure(2)
hold on
plot(t,yeuler(2,:),'b');
plot(t,y45(:,2),'r');
hold off
legend('Euler Impl\''icito','ode45');


Published with MATLAB® R2017a