CÁLCULO NUMÉRICO (521230)

LABORATORIO 6 - 2017-2

Integración Numérica

Contents

EJERCICIO 1

1.2 Testee su programa con las siguientes integrales y 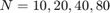$N = 10,20,40,80$:

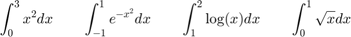
$$\int_0^3 x^2 dx \qquad \int_{-1}^1 e^{-x^2} dx \qquad \int_1^2 \log(x) dx \qquad \int_0^1 \sqrt{x} dx$$

clc;clear;close all
N = [10;20;40;80];
f_1=@(x)x^2;
f_2=@(x)exp(-x^2);
f_3=@(x)log(x);
f_4=@(x)sqrt(x);
for i=1:4
    I(i,1) = trap(f_1,0,3,N(i));
    I(i,2) = trap(f_1,-1,1,N(i));
    I(i,3) = trap(f_1,1,2,N(i));
    I(i,4) = trap(f_1,0,1,N(i));
end
format short
disp('I = ')
disp(I)

clc;clear;close all
N = [10;20;40;80];
f_1=@(x)x^2;
f_2=@(x)exp(-x^2);
f_3=@(x)log(x);
f_4=@(x)sqrt(x);
for i=1:4
    I(i,1) = simpson(f_1,0,3,N(i));
    I(i,2) = simpson(f_1,-1,1,N(i));
    I(i,3) = simpson(f_1,1,2,N(i));
    I(i,4) = simpson(f_1,0,1,N(i));
end
format short
disp('I = ')
disp(I)

EJERCICIO 2

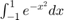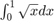2.2 Calcule mediante quad las integrales $\int_{-1}^1 e^{-x^2}dx$ y $\int_0^1 \sqrt{x} dx$ del Ejercicio 1.2, primero con la tolerancia prefijada por el comando y después con error menor que $10^{-6}$.

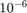clc;clear;close all

f_1 = @(x)exp(-x.^2);
f_2 = @(x)sqrt(x);

I(1,1) = quad(f_1,-1,1);
I(2,1) = quad(f_1,-1,1,1e-10);
I(1,2) = quad(f_2,0,1);
I(2,2) = quad(f_2,0,1,1e-10);
format long
disp('I = ')
disp(I)

I = 
   1.493648276062878   0.666659569272020
   1.493648265653887   0.666666666030499

EJERCICIO 4

4.1 Haga un programa que calcule la integral 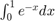$\int_0^1 e^{-x}dx$ por la regla de los trapecios con 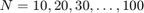$N = 10,20,30,\ldots,100$ subintervalos y almacene los errores respectivos. En este caso, para calcular el error utilice el valor verdadero de la integral, el cual puede calcularse exactamente.

clc;clear;close all
e = exp(1);
vreal = (e-1)/e;
N = 10:10:100;
f = @(x)exp(-x);
for i=1:10
    err(i) = abs(vreal - trap(f,0,1,N(i)));
end

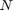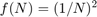4.2 Grafique en escala logarítmica estos errores versus $N$ y la función $f(N) = (1/N)^2$.

Sugerencia: para graficar en escala logarítmica utilice el comando loglog en lugar de plot; la sintaxis de ambos comandos es la misma.

loglog(N,err,'r',N,(1./N).^2,'b');
title('Error de integraci\''on');
legend('Error','$O(h^2)$')

EJERCICIO 5

5.1 Repita el ejercicio anterior con la integral 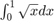$\int_0^1 \sqrt{x} dx$.

clc;clear;close all
vreal = 2/3;
N = 10:10:100;
f = @(x)sqrt(x);

for i=1:10
    err(i) = abs(vreal - trap(f,0,1,N(i)));
end

figure
loglog(N,err,'r',N,(1./N).^2,'b');
legend('Error','$O(h^2)$')

5.2 Para estimar el orden de convergencia del método en este caso, determine por cuadrados mínimos las constantes 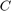$C$ y $\alpha$ que mejor ajustan los errores mediante el modelo

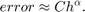
$$error \approx Ch^{\alpha}.$$

b = log(err)';
A = [ones(10,1) log(1./N)'];
x = A\b;
C = x(1);
alpha = x(2);
disp('alpha = ');
disp(alpha)

alpha = 
   1.481113215549433

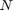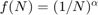5.3 Grafique en escala logarítmica los errores versus $N$ y la función $f(N) = (1/N)^{\alpha}$.

figure
loglog(N,err,'r',N,(1./N).^(alpha),'b');
title('Error de integraci\''on');
legend('Error','$O(h^\alpha)$')

EJERCICIO 6

6.1. Encuentre el área entre las curvas (x,f(x)) y (x,g(x)) con f(x) = exp(x - x^2), g(x) = arctan(x^2), x in [-3, 3].

clc;clear;close all
f = @(x)exp(x - x.^2);
g = @(x)atan(x.^2);

xx = linspace(-3,3);
plot(xx,f(xx),'b-',xx,g(xx),'r-');
grid on
legend('$f(x)$','$g(x)$');

h1 = @(x)f(x) - g(x); %dado que f > g
h2 = @(x)g(x) - f(x); %dado que g < f
a = fzero(h1,[-1 0]); %se puede encontrar las raíces de h1 o h2
b = fzero(h2,[1 2]);

area = quad(h2,-3,a) + quad(h1,a,b) + quad(h2,b,3);
disp('El área entre las curvas f y g es: ');
disp(area);

El área entre las curvas f y g es: 
   5.847004659652072

6.2 Encuentre todos los valores de x in [-3,3] tales que 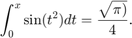$$\int_0^x \sin(t^2)dt = \frac{\sqrt{\pi)}}{4}.$$ Utilice para ello fzero y quad de manera adecuada.

clc;clear;close all
I = @(x)quad(@(t)sin(t.^2),0,x);
xx = linspace(-3,3);

plot(xx,arrayfun(I,xx),'b',[-3 3],[sqrt(pi)/4 sqrt(pi)/4],'r--');
grid on
legend({'$I(x)$','$\frac{\sqrt{\pi}}{4}$'},'FontSize',12,'Location','southeast');
grid on

v1 = fzero(@(x)I(x) - sqrt(pi)/4,1);
v2 = fzero(@(x)I(x) - sqrt(pi)/4,2.5);

fprintf('La función I(x), definida por la integral propuesta, alcanza el valor pedido en x = %f y x = %f \n',v1,v2);

La función I(x), definida por la integral propuesta, alcanza el valor pedido en x = 1.145941 y x = 2.434710

EJERCICIO 7

7.2 Pruebe su función para distintos valores 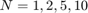$N = 1,2,5,10$ y las siguientes funciones:

Observe qué ocurre a medida que crecen los valores de 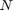$N$.

clc;clear;close all
f_1 = @(x)ones(1,numel(x));
f_2 = @(x)x;
f_3 = @(x)(x < 0).*1 + (x >= 0).*x.^2;

N = [1;2;5;10];

figure
k = linspace(0,1,1000);
hold on
plot(k,f_1(k),'k','linewidth',0.5)
for i=1:numel(N)
    SFn(f_1,0,1,N(i))
end
hold off
legend('$f(x)$','$SF_1$','$SF_2$','$SF_5$','$SF_{10}$')

figure
k = linspace(-1,2,1000);
hold on
plot(k,f_2(k),'k','linewidth',1.5)
for i=1:numel(N)
    SFn(f_2,-1,2,N(i))
end
hold off
legend('$g(x)$','$SF_1$','$SF_2$','$SF_5$','$SF_{10}$')

figure
k = linspace(-2,1,1000);
hold on
plot(k,f_3(k),'k','linewidth',1.5)
for i=1:numel(N)
    SFn(f_3,-2,1,N(i))
end
hold off
legend('$h(x)$','$SF_1$','$SF_2$','$SF_5$','$SF_{10}$')

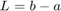7.3 Modifique la función anterior para que calcule la Suma parcial de Fourier en el intervalo $[a,b]$, pero que grafique dicha suma en el intervalo $[a-L,b+L]$, con $L = b - a$. ¿Qué se puede observar?

Cambiando el linspace de SFn, de k = linspace(a,b,1000) a k = linspace(a - L, b + L,1000), en una función SFn2, tenemos:

figure
k = linspace(0,1,1000);
hold on
plot(k,f_1(k),'k','linewidth',0.5)
for i=1:numel(N)
    SFn2(f_1,0,1,N(i))
end
hold off
legend('$f(x)$','$SF_1$','$SF_2$','$SF_5$','$SF_{10}$')

figure
k = linspace(-1,2,1000);
hold on
plot(k,f_2(k),'k','linewidth',1.5)
for i=1:numel(N)
    SFn2(f_2,-1,2,N(i))
end
hold off
legend('$g(x)$','$SF_1$','$SF_2$','$SF_5$','$SF_{10}$')

figure
k = linspace(-2,1,1000);
hold on
plot(k,f_3(k),'k','linewidth',1.5)
for i=1:numel(N)
    SFn2(f_3,-2,1,N(i))
end
hold off
legend('$h(x)$','$SF_1$','$SF_2$','$SF_5$','$SF_{10}$')

EJERCICIO 8

Escriba un rutero MATLAB en el que:

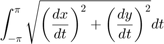
$$\int_{-\pi}^{\pi} \sqrt{\left( \frac{dx}{dt}\right)^2 + \left( \frac{dy}{dt} \right)^2}dt$$

clc;clear;close all
x = @(t)3*cos(t);
y = @(t)5*sin(t);
t = linspace(-pi,pi,200);
plot(x(t),y(t),'m');
title('Elipse')
axis([-5 5 -5 5])
grid on

p = @(t)(sqrt((-3.*sin(t)).^2 + (5.*cos(t)).^2));
per = quad(p,-pi,pi);
disp('El perímetro de la elipse es =')
disp(per)

El perímetro de la elipse es =
  25.526998885744735

FUNCIONES

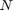1.1 Escriba en un archivo trap.m un programa tipo function que calcule la aproximación de la integral de una función dada en un intervalo genérico $[a,b]$ por la regla de los trapecios con $N$ subintervalos.

function int = trap(f,a,b,N)
h = (b-a)/N; %tamaño de paso
x = a:h:b;
sum = 0; %variable que almacena el valor de la suma
for i=2:N %considerar que x(1) = a, x(2) = a + h, ... x(N) = b - h
   sum = sum + f(x(i));
end
int = h*((f(a)+f(b))/2 + sum);
end

I = 
    9.0450    0.6800    2.3350    0.3350
    9.0112    0.6700    2.3337    0.3337
    9.0028    0.6675    2.3334    0.3334
    9.0007    0.6669    2.3334    0.3334

1.3 Haga un programa semejante para la regla de Simpson. Guárdelo en un archivo simpson.m y testeelo con las mismas funciones.

function int = simpson(f,a,b,N)
x = linspace(a,b,2*N+1);
sumi = f(x(2*N)); %suma impar, con valor inicial f(x_2n-1)
sump = 0; %suma par
for i=3:2:(2*N)-1
    sumi = sumi + f(x(i-1));
    sump = sump + f(x(i));
end
int = ((b-a)/(2*N))/3 * (f(a) + f(b) + 4*sumi + 2*sump);
end

I = 
    9.0000    0.6667    2.3333    0.3333
    9.0000    0.6667    2.3333    0.3333
    9.0000    0.6667    2.3333    0.3333
    9.0000    0.6667    2.3333    0.3333

Versión alternativa

function int = simpson2(f,a,b,N)
h = (b-a)/(2*N);
x = a:h:b;
sumi = 0; %suma impar, notar que nodos impares son pares pues x_1 <-> x(2)
for i = 2:2:(2*N - 1)
    sumi = sumi + f(x(i));
end
sump = 0; %suma par, notar que nodos pares son impares pues x_2 <-> x(3)
for i = 3:2:(2*N - 2)
    sump = sump + f(x(i));
end
int = (h/3) * (f(a) + f(b) + 4*sumi + 2*sump);
end

Versión alternativa (2)

function int = simpson3(f,a,b,N)
h = (b-a)/(2*N);
sumi = 0; %suma impar, notar que nodos impares son pares pues x_1 <-> x(2)
for i = 1:N
    sumi = sumi + f(a + (2*i-1)*h);
end
sump = 0; %suma par, notar que nodos pares son impares pues x_2 <-> x(3)
for i = 1:N-1
    sump = sump + f(a + (2*i)*h);
end
int = (h/3) * (f(a) + f(b) + 4*sumi + 2*sump);
end

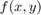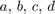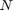EJERCICIO 3 Escriba un programa tipo function en MATLAB que reciba como entrada una función de 2 variables $f(x,y)$, y los valores $a,\, b,\, c,\, d$ y $N$ y cuya salida sea el valor de la integral:

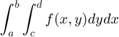
$$ \int_a^b \int_c^d f(x,y)dydx $$

donde la integral respecto a 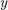$y$ sea resuelta mediante la regla de los trapecios y la integral con respecto a $x$ sea resuelta con la regla de Simpson.

function int = intmultiple(f,a,b,c,d,N)
X = linspace(a,b,N+1);
Y = linspace(c,d,N+1);
h1 = (b-a)/N;
h2 = (d-c)/N;
A = [h1/2 h1/2];
B = [h2/6 4*h2/6 h2/6];
int = 0;
for s1 = 1:N
    for s2 = 1:N
        x = [X(s1) X(s1+1)];
        y = [Y(s2) (Y(s2)+Y(s2+1))/2 Y(s2+1)];
        for i=1:2
            for j=1:3
                int = int + A(i)*B(j)*f(x(i),y(j));
            end
        end
    end
end
end

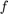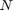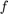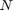7.1 Escriba una función en MATLAB cuyas entradas sean $f$, el intervalo $[a,b]$ y $N$. Esta función debe dibujar en un mismo gráfico $f$ y la $N$-ésima Suma Parcial de Fourier en el intervalo $[a,b]$.

function SFn(f,a,b,N)
   L = (b-a);
   a_0 = 2/L * integral(f,a,b);

   for n = 1:N
    a_n(n) = 2/L * integral(@(x)f(x).*cos((2*pi/L)*n*x),a,b);
    b_n(n) = 2/L * integral(@(x)f(x).*sin((2*pi/L)*n*x),a,b);
   end

   SF = @(x)a_0/2 + sum(a_n.*cos((2*pi/L)*(1:N).*x)) + sum(b_n.*sin((2*pi/L)*(1:N).*x));

   pp = linspace(a,b,250);
   plot(pp,arrayfun(SF,pp),'--');
end

7.3 Modifique la función anterior (...)

function SFn2(f,a,b,N)
   L = (b-a);
   a_0 = 2/L * integral(f,a,b);

   for n = 1:N
    a_n(n) = 2/L * integral(@(x)f(x).*cos((2*pi/L)*n*x),a,b);
    b_n(n) = 2/L * integral(@(x)f(x).*sin((2*pi/L)*n*x),a,b);
   end

   SF = @(x)a_0/2 + sum(a_n.*cos((2*pi/L)*(1:N).*x)) + sum(b_n.*sin((2*pi/L)*(1:N).*x));
   pp = linspace(a-L,b+L,250);
   plot(pp,arrayfun(SF,pp),'--');
end


Published with MATLAB® R2017a