CÁLCULO NUMÉRICO (521230)
LABORATORIO 5 - 2017-2
Mínimos Cuadrados
Contents
EJERCICIO 1
1.2 Escriba un rutero en MATLAB en el que haga lo siguiente:
- Construya la matriz A y parte derecha y del sistema de ecs. lineales.
- Resuelva el sistema Ac = y en el sentido de los mínimos cuadrados.
- Grafique en un mismo gráfico los pares en la tabla y el polinomio obtenido (evaluado en 100 puntos entre 0 y 8 con ayuda de polyval).
Recordar que el ajuste para este ejercicio era por un polinomio de grado menor o igual a 2. Es decir, de la forma
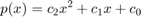
clc;clear;close all %%DATOS x = [0.0;1.0;2.0;3.0;4.0;5.0;6.0;7.0;8.0]; %en columnas!! y = [12.0;10.5;10.0;8.0;7.0;8.0;7.5;8.5;9.0]; %%AJUSTE A = [x.^2 x ones(size(x))]; b = y; c = A\b; %notar que c corresponde a los coeficientes del polinomio, en el orden "correcto" (mayor coef. a menor).% %%GRÁFICO xx = linspace(min(x),max(x)); figure hold on plot(x,y,'bx','MarkerSize',11) %datos experimentales plot(xx,polyval(c,xx),'r') %ajuste por mínimos cuadrados hold off xlabel('Aditivo (en gramos)') ylabel('Tiempo de secado (en horas)') legend('Datos experimentales','Ajuste polinomial') grid on

EJERCICIO 2
2.2 Escriba un rutero en MATLAB que haga lo siguiente:
- Construya la matriz A y parte derecha y del sistema de ecs. lineales.
- Resuelva el sistema Ac = y en el sentido de los mínimos cuadrados.
- Grafique en un mismo gráfico los pares en la tabla y la funcióon p(t) obtenida.
- En base a la función obtenida, ¿cuál es el número de microorganismos que había en la muestra inicialmente? ¿y después de una hora y media? ¿y después de 5 horas y media?
Notar que el ajuste no es polinomial, sino de acuerdo al modelo:
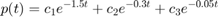
clc;clear;close all %%DATOS t = [0.5;1;2;3;4]; p = [7;5.2;3.8;3.2;2.5]; %%AJUSTE A = [exp(-1.5*t) exp(-0.3*t) exp(-0.05*t)]; b = p; c = A\b; fun = @(t) c(1)*exp(-1.5*t) + c(2)*exp(-0.3*t) + c(3)*exp(-0.05*t); %%GRÁFICO tt = linspace(min(t),max(t)); figure hold on plot(t,b,'bx','MarkerSize',13) plot(tt,fun(tt),'r') hold off xlabel('Tiempo (en horas)') ylabel('Número de microorganismos (en miles)') legend('Datos experimentales','Ajuste funcional') grid on %EXTRA m1 = fun(0); m2 = fun(1.5); m3 = fun(5.5); fprintf('Al inicio habían %2.0f microorganismos, luego de una hora y media habían %2.0f y al cabo de cinco horas y media, %2.0f',m1,m2,m3);
Al inicio habían 10 microorganismos, luego de una hora y media habían 4 y al cabo de cinco horas y media, 2

EJERCICIO 3
Escriba un rutero en MATLAB que ejecute las siguientes tareas:
- Determine los parámetros
 y
y 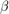 que ajustan ambos modelos a los datos de la tabla en el sentido de los mínimos cuadrados. Su programa debe mostrar estos parámetros.
que ajustan ambos modelos a los datos de la tabla en el sentido de los mínimos cuadrados. Su programa debe mostrar estos parámetros. - Para ambos modelos, muestre
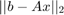 del sistema
del sistema 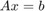 que su programa resuelve.
que su programa resuelve. - Dibuje en un mismo gráfico los datos de la tabla y ambos modelos ajustados.
- Con el mejor modelo, estime qué porcentaje de las llantas radiales del fabricante durarán 45000 millas y 50000 millas. Su programa debe mostrar estas estimaciones.
clc;clear;close all %%DATOS x = [1;2;5;15;25;30;35;40]; y = [99;95;85;55;30;24;20;15]; %MODELO 1% A1 = [ones(size(x)) x]; b1 = log(y); c1 = A1\b1; alf1 = exp(c1(1)); bet1 = exp(c1(2)); fun1 = @(x) alf1.*bet1.^x; err1 = norm(b1 - A1*c1); %notar que norm(x) := norm(x,2)%; fprintf(1,'Los parámetros para el modelo 1 son:\n'); fprintf(1,'Alfa_1 = %f\n',alf1); fprintf(1,'Beta_1 = %f\n',bet1); fprintf(1,'El error del modelo 1 es: %f\n\n',err1); %MODELO 2% A2 = [ones(size(x)) x]; %esta línea es redundante, notar que la matriz A es válida en ambos modelos% b2 = log10(y./(100-x)); c2 = A2\b2; alf2 = 10^(c2(1)); bet2 = c2(2); fun2 = @(x) alf2.*(100 - x).*10.^(bet2*x); err2 = norm(b2 - A2*c2); fprintf(1,'Los parámetros para el modelo 2 son:\n'); fprintf(1,'Alfa_2 = %f\n',alf2); fprintf(1,'Beta_2 = %f\n',bet2); fprintf(1,'El error del modelo 2 es: %f\n\n',err2); %MEJOR MODELO %GRÁFICO% xx = linspace(0,50,250); figure hold on plot(x,y,'bx'); plot(xx,fun1(xx),'r'); %MODELO 1 plot(xx,fun2(xx),'g'); %MODELO 2 hold off xlabel('Millas recorridas (en miles)') ylabel('Porcentaje útil') legend('Datos experimentales','Ajuste modelo 1','Ajuste modelo 2') grid on %EXTRA p45 = fun2(45); p50 = fun2(50); fprintf('El porcentaje de las llantas radiales del fabricante que durarán 45000 millas y 50000 son %3.2f %% y %3.2f %%, respectivamente',p45,p50);
Los parámetros para el modelo 1 son: Alfa_1 = 106.536204 Beta_1 = 0.952375 El error del modelo 1 es: 0.102423 Los parámetros para el modelo 2 son: Alfa_2 = 1.052490 Beta_2 = -0.015721 El error del modelo 2 es: 0.044552 El porcentaje de las llantas radiales del fabricante que durarán 45000 millas y 50000 son 11.35 % y 8.61 %, respectivamente

EJERCICIO 4
Escriba un rutero MATLAB que,
- Encuentra la función de la forma
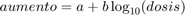
que mejor ajusta por cuadrados mínimos los datos dados.
- Grafique en un mismo gráfico los pares en la tabla y la función obtenida (evaluada en 100 puntos entre 0.25 y 7.5).
- Basado en la función obtenida, ¿qué cantidad de vitamina A es requerida para no aumentar de peso?
clc;clear;close all %%DATOS x = [0.25;1.0;1.5;2.5;7.5]; y = [-10.8;13.5;16.4;28.7;51.3]; %%AJUSTE A = [ones(size(x)) log10(x)]; c = A\y; a = c(1); b = c(2); fun = @(x) a + b*log10(x); %%GRÁFICO xx = linspace(0.25,7.5); hold on plot(x,y,'bx'); plot(xx,fun(xx),'r'); hold off xlabel('Dosis de vitamina A (en mg)') ylabel('Aumento de peso (en g)') legend('Datos experimentales','Ajuste funcional','location','southeast') grid on

EJERCICIO 5
5.1 Muestre que existe una relación lineal entre 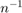 y
y  .
.
Dada la relación
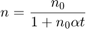
Podemos reescribirla en forma lineal (para 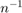 y
y  ) como:
) como:
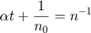
5.2 Encuentre la función que mejor ajusta por cuadrados mínimos a los datos en la tabla. Escriba las aproximaciones a 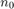 y
y  obtenidas.
obtenidas.
5.3 Grafique los pares ordenados en la tabla y la función  obtenida (evaluada en 110 puntos entre 0 y 10)
obtenida (evaluada en 110 puntos entre 0 y 10)
clc;clear;close all %%DATOS t = (0:10)'; n = 1e-4*[5.03;4.71;4.40;3.97;3.88;3.62;3.30;3.15;3.08;2.92;2.70]; %%AJUSTE A = [t ones(size(t))]; b = 1./n; c = A\b; alfa = c(1); n0 = 1/c(2); fun = @(t) n0./(1 + n0*alfa*t); fprintf('La concentración inicial de iones es %e y el coeficiente de recombinación, %f\n',n0,alfa) tt = linspace(0,10,110); hold on plot(t,n,'x') plot(tt,fun(tt),'r') hold off xlabel('Tiempo (en s)') ylabel('Concentración de iones') legend('Datos experimentales','Ajuste funcional') grid on
La concentración inicial de iones es 5.095600e-04 y el coeficiente de recombinación, 167.915510
