CÁLCULO NUMÉRICO (521230)

LABORATORIO 2 - 2017-2

Programas en MATLAB

Contents

EJERCICIO 1

Escriba una función en MATLAB que para una entrada 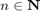$n \in \bf{N}$ ejecute las siguientes tareas:

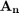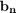  1. Construya la matriz $\mathbf{A_n}$ y el vector $\mathbf{b_n}$.
  2. Resuelva el sistema 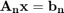$\mathbf{A_n x = b_n}$ con el comando x = A\b
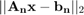
  3. Devuelva como salida el valor $||\mathbf{A_n x - b_n}||_2$
function E = lab2_ejercicio1(n)
A = diag(1:(n-1),1) + diag(1:(n-1),-1) + diag(n:-1:1);
b = (1:n)./(n:-1:1);
x = A\b;
E = norm(A*x - b,2);
end

A continuación se presenta una manera alternativas de definir el cuerpo de la función, utilizando el valor de referencia n = 5 y en formato rutero.

clc
clear all
n = 5;
A = zeros(n);
b = zeros(n,1);
for i = 1:n-1
    A(i,i) = n + 1 - i; %esto funciona como contador "al revés"
    A(i+1,i) = i;
    A(i,i+1) = i;
    b(i) = i/(n + 1 - i);
end
A(n,n) = 1; %como el ciclo for está diseñado para funcionar hasta (n-1,n-1), agregamos la última componente a mano
b(n) = 1/n; %alternativamente, se puede hacer un ciclo for aparte para construir b
disp('A = '), disp(A);
disp('b = '), disp(b);

A = 
     5     1     0     0     0
     1     4     2     0     0
     0     2     3     3     0
     0     0     3     2     4
     0     0     0     4     1

b = 
    0.2000
    0.5000
    1.0000
    2.0000
    0.2000

EJERCICIO 2

Sea

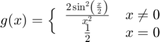
$$g(x) = \Big\{ \begin{array}{cc} \frac{2\sin^2\left(\frac{x}{2}\right)}{x^2} & x \neq 0 \\ \frac{1}{2} & x = 0 \end{array}$$

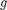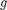Escriba una función mifuncion2 para evaluar $g$ en las componentes de un vector de entrada $x$. Evalúe a $g$ en [0.188e-7, 0.189e-7, 0.19e-7].

function G = mifuncion2(x)
for i = 1:length(x)
    if x(i) ~= 0
        G(i) = (2*(sin(x(i)/2))^2)/x(i)^2;
    else
        G(i) = 0.5;
    end
end
end

x = [0.188e-7, 0.189e-7, 0.19e-7];
val = mifuncion2(x);
disp(val)

    0.5000    0.5000    0.5000

EJERCICIO 3

Escriba un programa MATLAB, tipo function, que para 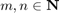$m,n \in \bf{N}$ dados, genere la matriz 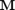$\mathbf{M}$ y vector 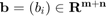$\mathbf{b} = (b_i) \in \bf{R}^{m+n}$, cuyas componentes están dadas por 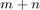$m+n$ primeros componentes de la sucesión convergente al número de Euler $e$.

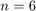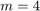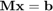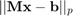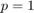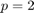Luego, en un programa tipo rutero, llame a la función con $n = 6$ y $m = 4$, resuelva el sistema $\mathbf{Mx = b}$ y calcule $||\mathbf{Mx - b}||_p$, para $p = 1$, $p = 2$ y $p = \infty$.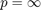

function [M,b] = lab2_ejercicio3(m,n)

vm = m:-1:1;
vn = n:-1:1;

Am = diag(vm); Am(1,:) = vm; Am(:,1) = vm;
An = diag(vn); An(1,:) = vn; An(:,1) = vn;

Z = zeros(m,n);

M = [Am Z;
    Z' An];

b = zeros(m+n,1);
for i = 1:(m+n)
    b(i) = (1 + 1/i)^i;
end

end

clc
clear all
[M,b] = lab2_ejercicio3(4,6);
x = M\b;
Np = zeros(3,1);
for p = [1,2,Inf]
    Np = norm(M*x - b,p);
    fprintf('||Mx - b||_%i = %e \n',p,Np);
end

||Mx - b||_1 = 3.108624e-15 
||Mx - b||_2 = 1.332268e-15 
||Mx - b||_Inf = 8.881784e-16


Published with MATLAB® R2017a