II. TEORIA DE GRAFOS
El grafo G es un par G = (V,Î ) donde V es un conjunto finito de Nodos o Vértices y Î tiene como elementos subconjuntos de V de cardinalidad los denominados aristas los vértices de V generalmente son denominados 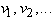 Ejemplo el grafo:
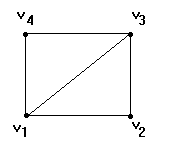
Ejemplo el grafo:
G=( {v1,v2,v3.v4},{ [v1,v2] ,[v2,v3], [v3,v4],[v4,v1],[v1,v3]})
Multigrafos ; Grafos con Aristas repetidas
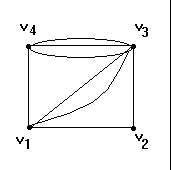
Formalmente un digrafo D es un par D=(V,A), donde V es un conjunto de vértices
Grafos direccionado o digrafo es un grafo con direcciones asignadas a sus aristas. A es un conjunto de pares de vértices denominados arcos o sea A Í V x V
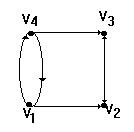
D={v1,v2,v3,v4},{(v1,v2),(v2,v3),(v4,v3),(v4,v1),(v1,v4),(v1,v3)})
G = (V, E) es un Grafo y e=(v1,v2) Î E, entonces diremos 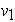 es adyacente a
es adyacente a 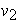 (o viceversa) y que es incidente a
(o viceversa) y que es incidente a 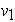 (y
(y 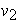 ). El grado de un vértice v Î G es el número de arcos incidente a v. En el grafo el grado de
). El grado de un vértice v Î G es el número de arcos incidente a v. En el grafo el grado de 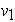 es 3.
es 3.
En el digrafo D = (V,A) el grado entrada de un nodo v es el nº de arcos de la forma (u, v) que están en A. El grado de salida es el nº de arcos que tienen la forma (v,u)
Suponga que B = (W, E) es un grafo que tiene la siguiente propiedad que el conjunto de vértices W puede ser particionado en dos conjuntos V y U y cada arista en E tiene un vértice en V y uno vértice en U. Entonces B es denominado Grafo Bipartito.

Grafos Dirigidos
El grafo G = [V,A]
Conjunto de Conjunto de pares ordenados de vértices
nodos o vértices 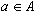 llamados arcos.
llamados arcos.
Si : N = ½ V ½ es el número de vértices, entonces se dice que el grafo es del orden N en vértices son numerados de i=1,...,N
Si a= (i,j) es un arco de G, entonces i es el punto inicial de u y j es el punto terminal de u. En general se dice que ½ A½ =M
Gráficamente los vértices se representan los puntos y los arcos a=(i,j) es representado por un arreglo conectando los punto i y j (j el tope del arreglo).
Arcos con coincidencia de puntos finales se llama loop.
Un p-grafo es un grafo con no más de p arcos (i,j) entre dos pares cualquiera de vértices i y j.
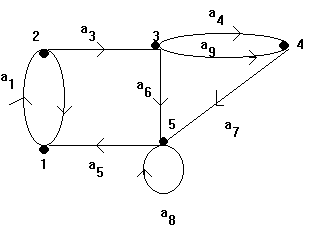
a8=(5,5) es un loop
2. Grafo, ya que a4 y a9 son (3,4)
j es sucesor de i si existe arco con i inicial y j terminal. Los sucesores de un vértice i Î V es denominado por 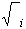
j es antecesor de i si existe un arco de la forma (j,i), el conjunto de los antecesores es 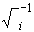
Grafos no dirigidos
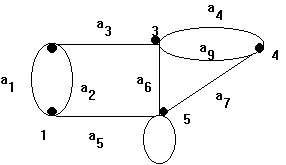
Multigrafos grafos donde más que una arista puede existir entre dos vértices. Grafo simple si no existe loop y si nunca existe más que una arista entre dos vértices.
Dos arcos o aristas son llamados adyacentes si existe al menos un punto común entre ellas.
Grado de un vértice.
dG (i) = dG++(i)+dG-- (i)
para el nodo 2 de la primera figura:
d+(2)=2 , d-(2)=1 Þ d(2) =3
Cociclo de un Grafo
w (A)= w+ £ (A) + w- - (A)
w : Conjunto de arcos de esta forma es denominado Cociclo.
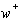 : Conjunto de arcos con inicio en A y término en A=X-A
: Conjunto de arcos con inicio en A y término en A=X-A
Grafos Simétricos _
Si para todos los pares de vértices (i,j) existen muchos arcos de la (i,j) como muchos de la forma (i,j).
Grafos Asimétricos
Un 1 - grafo G=(V,A) es asimétrico cuando:
(i,j) Î A U Þ (j,i) 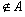
Grafo Completo. Clique
Si para todos los pares de vértices (i,j) existe un arista de la forma (i,j)
1.- Grafo es completo s si
(i,j)Î A ® (j,i) Î A
Un grafo completo de orden N es denominado por KN. Un subconjunto de vértices 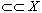 tal que cualquier dos vértices de C son conectados por una arista es llamado Clique.
tal que cualquier dos vértices de C son conectados por una arista es llamado Clique.
Si dos grafos: G1 (V1, A1) , G2 (V2, A2). Con ½ V1½ = ½ V2½ =M existe una función unívoca f: V1 ® V2, tal que (v,w) Î A1 ssi (f(V), f(w))Î 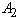 , para todo v,w, Î A1. si es positivo G1 Y G2 Son isomorfos
, para todo v,w, Î A1. si es positivo G1 Y G2 Son isomorfos
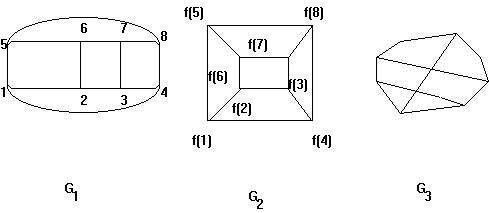
No existe función f que haga coincidir las representaciones G1 y G3, G3 no es isomorfo a G1 ni G2.
El problema de Isomorfismo puede ser resuelto naturalmente por "Fuerza Bruta", o búsqueda exhaustiva examinando cada una de las n¡ permutaciones de V1 (o sea cada función f). Este algoritmo necesitaría 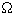 (n!) pasos en el peor caso.
(n!) pasos en el peor caso.
No existe otro algoritmo general eficiente para esto.
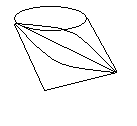
Grado de un vértice v E V, "grado (v)" es el número de vértices adyacentes a v. Grafo regular de grado r, cuando todos los vértices poseen el mismo grado. El ejemplo es regular de grado 3. Vértice.
Secuencia de vértices v1,...,vk tal que (vj,vj+1) E A, 1 £ J < ³k-1³ es denominado camino de vj a vk. Un camino de K vértices es formado por k-1 aristas (v1, v2), (v2,v3),...,(vk-1, vk). El valor k-1 es el largo del camino.
Si todos los vértices fueran diferentes a la secuencia el camino es un camino elemental. Si todas las aristas fueran diferentes a la secuencia se trata de una trayectoria. En la figura anterior C1= { 1,2,3,7} es un camino simple; C2= { 2,3,7,6,2,1} es una trayectoria. Un ciclo es un camino donde V1,...,Vk,VK+1 y V1=Vk+1 con k>3. Si el camino es simple el ciclo también es simple (v1,...,vk, Kk+1). Un grafo sin ciclos simples es acilico. Triángulo es un ciclo de largo 3.
Camino hamiltoneano: Es un camino que contiene cada arista exactamente una sola vez.
Camino elulenario: Es un camino que contiene cada arista exactamente una sola vez.
Un ciclo V1,...,Vk,Vk+1 es hamiltoneano cuando el camino V1,...vk lo es.
En la figura anterior los ciclos.
2,3,7,6,2 y 7,6,2,3,7 son idénticos.
1,5,6,2,3,7,8,4 es un camino hamiltoneano.
Un grafo G (V,A) é denominado conexo cuando existe camino entre cada par de vértices de G. en C.C es desconexo. Un grafo G es totalmente desconectado cuando no posee aristas.
Si S un conjunto tal que S' Í S'. Diremos que S' es maximal en relación a una cierta propiedad P, cuando S' satisface la propiedad P y no existe subconjunto S"Ê S', que también satisfaz P. No necesariamente S' es el mayor subconjunto de S. satisfaciendo P. Igualmente se define Minimal. Se denomina componentes conexos de un grafo G a los Subgrafos Maximales de G que son conexos. La propiedad P es equivalente a ser conexo.
![]() Ejemplo el grafo:
Ejemplo el grafo:


![]() es adyacente a
es adyacente a ![]() (o viceversa) y que es incidente a
(o viceversa) y que es incidente a ![]() (y
(y ![]() ). El grado de un vértice v Î G es el número de arcos incidente a v. En el grafo el grado de
). El grado de un vértice v Î G es el número de arcos incidente a v. En el grafo el grado de ![]() es 3.
es 3.




