Grafos

Listado de Ejercicios Nº1

Resuelto

VERDADERO O FALSO, COMENTE LAS FALSAS.

Un grafo bipartito completo puede tener una clique. V

Todo grafo es simétrico. F, contraejemplo: P/

Un digrafo es un grafo con no más de dos aristas entre cada par de vértices. F, es un grafo dirigido.

Dos grafos son isomorfos entre sí cuando presentan tanto mismo número de vértices como de aristas. F, deben poseer ,además, igual conexión de vértices.

Un p-grafo es un grafo regular de grado p. F, donde al menos un par de vértices se encuentra conectado por tres aristas.

Todo grafo hamiltoneano es biconexo, luego todo grafo que no sea biconexo no puede ser hamiltoneano. V

Un grafo es bipartito si y sólo si todo ciclo en el grafo tiene longitud par. F, puede no tener ciclo.

Un subgrafo generado puede tener aristas distintas del grafo original. F, poda arista que poseea debe pertenecer al grafo original.

Un subgrafo inducido puede tener aristas distintas del grafo original. F, poda arista que poseea debe pertenecer al grafo original.

El orden de un grafo corresponde al número total de vértices del mismo. V

Circuito es igual a ciclo. F, en el ciclo el primer vértice del conjunto es igual al último, en un circuito no.

Loop es un circuito de longitud 1. V

El complemento de un grafo totalmente desconexo es siempre una clique. V

Un grafo bipartito completo posee un número par de vértices. F, ej. K23

Un grafo planar es aquel en que no existe entrecruzamiento de aristas. F, es el que puede ser representado sin entrecruzamiento de aristas.

Un grafo conectado con un número mínimo de aristas es un árbol.V

El grado de un vértice en un digrafo es la cantidad de arcos que salen de él menos los que llegan. F, los que salen menos los que llegan.

Todo grafo completo es regular. F, ej. K23

Un grafo bipartito con más de 5 vértices no puede ser planar. V

El complemento de un grafo conexo no puede tener ciclo hamiltoneano. F, si puede tener C.H.

Un grafo conexo no puede tener conjunto independiente. Todo grafo conexo tiene conjunto independiente de vértices.

Un grafo desconexo pude ser bipartito. V

No existe relación entre un grafo completo y una clique. F, Una clique es un subgrafo completo.

El problema del vendedor viajero consiste en encontrar un ciclo hamiltoneano de largo máximo. V

El número cromático de un grafo corresponde al número de vértices que posee el grafo. F, núm. cromático corresponde al número mínimo de colores, tal que cada vértice adyacente de un par tenga distinto color.

El número de aristas de un grafo, se obtiene de la combinación de m sobre 2, donde m es número de aristas. F, se obtiene por la combinación de n sobre 2, donde n es el número de vértices.

Un grafo es bipartito cuando el conjunto de aristas es particionado en tres subconjuntos. F, es bipartito cuando el conjunto de vértices es particionado en dos subconjuntos.

El problema del "Vendedor Viajero" está asociado con los ciclos Eulerianos. F, con Hamiltoneanos.

Kn es planar para 1<=n<=5. F, K5 no es planar.

Un árbol de n vértices tiene exactamente n-1 aristas. V

Un "corte de vértices" es un conjunto minimal. V

La representación planar satisface la relación n+f=m+2, donde: n es número de vértices, m es número de aristas y f es número de fases. V

Un grafo G(N;A) tal que |N|=5 y |A|=10 no puede tener número cromático igual a 4. V

Los siguientes grafos son isomorfos. V

Sea s un conjunto y S’ a S . Se dice que S’ es maximal para una propiedad P si: el conjuneto S’ satisface P y además no existe ningún conjunto S’’ a S que tambien satisface P tal que |S’’| > |S’|. F

Existe una gran relación entre los conceptos: "coloración de un grafo" y " número de conjuntos independientes de vértices". V

Los grafos K5 y K33 son planares, compruebe con la formula. F, en ningún caso se cumple la relación n+f=m+2.

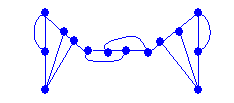
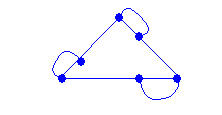
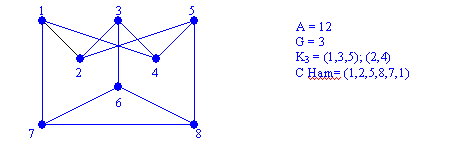
CONSTRUYA UN GRAFO CON LAS SIGUIENTES CARACTERÍSTICAS.

grafo planar, regular de grado 3, biconexo y no hamiltoneano.

Grafo 3-conexo, planar y no hamiltoneano.

Grafo con conectividad de vértices 2, conectividad de aristas 3, número cromático igual a 3 y regular de grado 3.

1-grafo, V=8, A<=14, Grado (v) <=4 para todo vértice en V, debe poseer como subgrafo un K_3,2, posea un grafo de orden 5 que sea hamiltoneano.

Dibuje un grafo (simple y sin loop) tal que su número cromático sea distinto a la cardinalidad de la clique máxima.

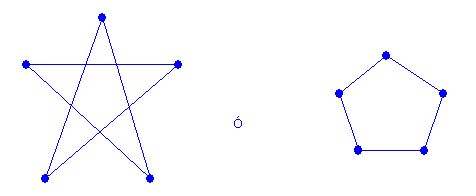
DEMOSTRACIONES.

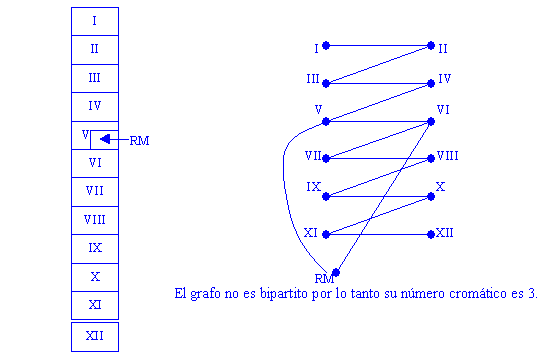
Demuestre que todo grafo bipartito conexo con número impar de vértices no es hamiltoneano.

En cualquier caso de número impar de vértices, si se parte desde un conjunto para volver al mismo vértice, es paso exactamente anterior será estar en un vértice del mismo conjunto y si se unieran los vértices del mismo conjunto para hacerlo Hamiltoneano, dejará de ser un grafo bipartito.

Demuestre que un grafo G es bicoloreable sí y sólo sí si fuera bipartito.

Si es bicoloreable, posee Cv=2 por lo tanto es bipartito.

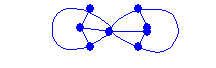
GRAFOS ISOMORFOS.

Indique si los pares de grafos son isomorfos o no, argumente su respuesta.

CORTE DE VÉRTICES Y DE ARISTAS.

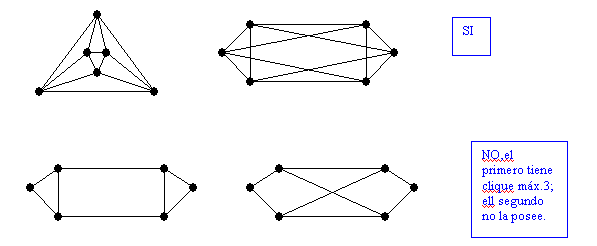
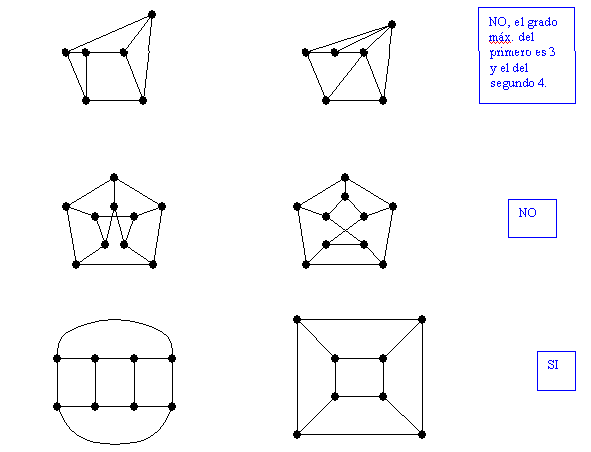
Encuentre el corte de vértices y de aristas.

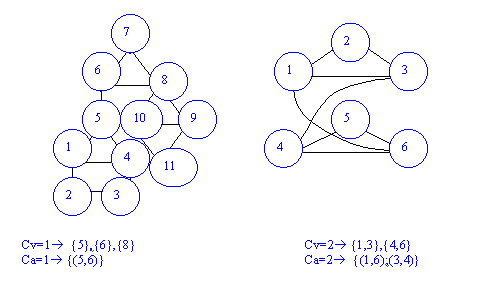
DETERMINE EL NÚMERO CROMÁTICO DE:

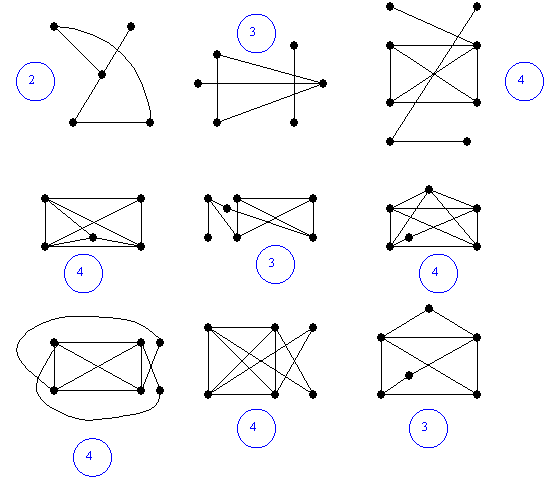
MULTIPLES:

Para el grafo de la figura indique:

Cardinalidad de vértices.
Cardinalidad de aristas.
Complemento del grafo.
Grado de cada vértice.
El grafo es regular?.
Encontrar un conjunto independiente de tamaño 4.
Encontrar un clique de tamaño 4.

#V = 9

#A = 14

G(A) = 5, G(B) = 1, G(C) = 3, G(D) = 2, G(E) = 4, G(F) = 3, G(G) = 2, G( H) = 3, G(I) = 5.

No es regular, por d) no todos los vértices tienen el mismo grado.

CI = {D,H,F,G}

Clique = {A,C,F,I}

Para el grafo ,encuentre:

Las conectividades en vétices y aristas. Justifique su respuesta.
Este grafo ¿ es 1-conexo o 2-conexo en aristas? . Justifique su respuesta.

Ca = 2à { (3,5),(4,5)}; Cv = 1à {5}

2 conexo.

Considere el grafo que posee la siguiente matriz de adyacencia:

1 2 3 4 5 6

1 | 0 0 1 1 0 1

2 | 0 0 1 1 1 0

3 | 1 1 0 0 1 1

4 | 1 1 0 0 1 0

5 | 0 1 1 1 0 0

6 | 1 0 1 0 0 0

Dibuje el grafo.
Muestre la mayor clique.
Muestre una clique maximal que no sea máxima.
¿Cuál es la conectividad vértice y conectividad arista del grafo?. Justifique adecuadamente su respuesta.

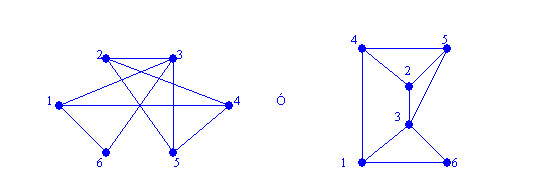
b) la mayor clique es K₃, puede ser cualquiera de los siguientes tres conjuntos de vértices:

(2,4,5); (2,3,5); (1,3,6).

para el ciclo (1,3,2,4,1), la clique maximal es {1,4} que no es máxima.

Cv= 2 à {4,3} ó {3,1}; Ca= 2 à {(1,6),(3,6)}

Dibuje el grafo correspondiente al mapa de Chile, considerando que el país se divide en 13 regiones. ¿Cuál es el número cromático de este grafo?.

Representación gráfica. Grafo correspondiente.

Encuentre una expresión para el número de vértices posibles en un árbol binario que tiene los niveles 0,1...k.

Cuál es el grado de cada vértice: todos los demás grado 3.

PROFUNDIDAD Y ANCHURA.

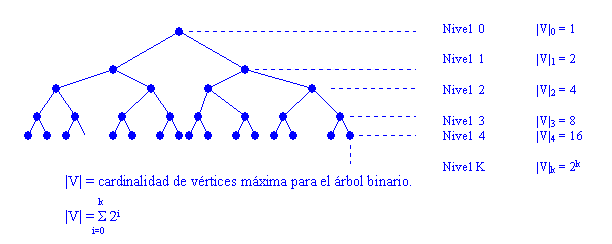
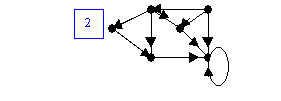
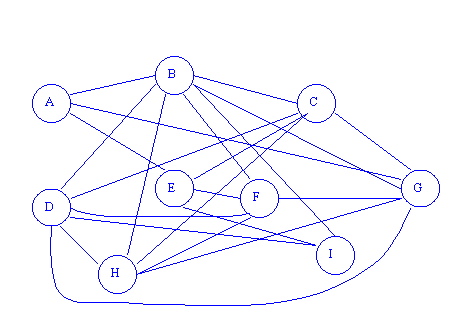
Para el siguiente grafo, determine su árbol de profundidad y de anchura.

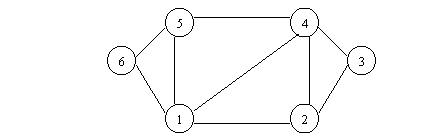
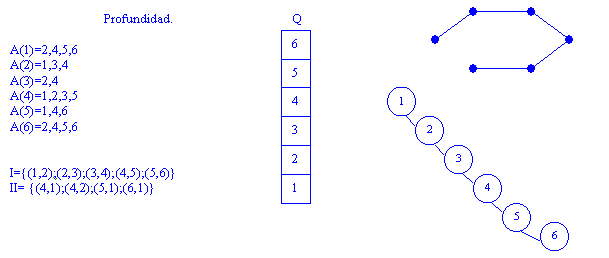
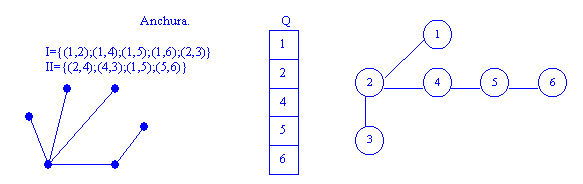
Podría indicar ¿qué listas de adyacencia del grafo a) generan el grafo de profundidad

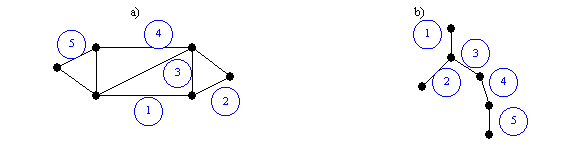
PRIM Y KRUSCAL.

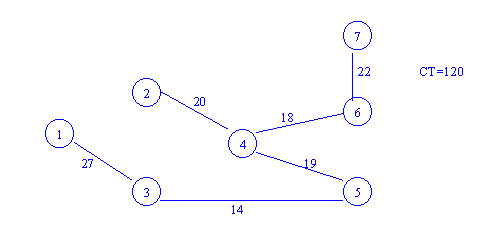
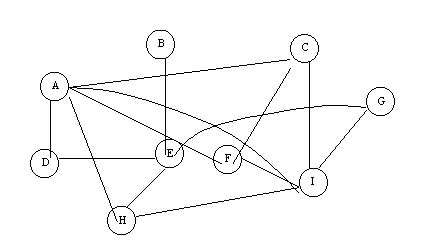
Dado el grafo, obtener el árbol de expansión mínimo mediante los algoritmos de Prim y Kruscal.

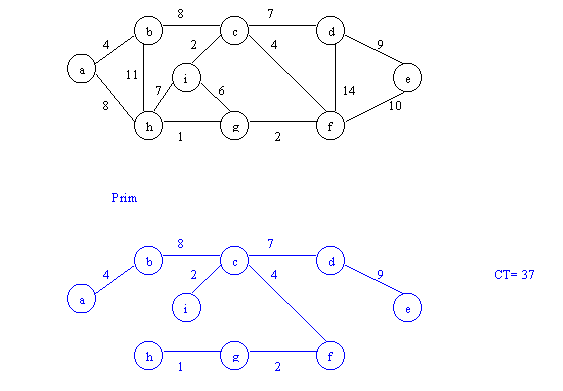
Kruscal

{ (h,g);(g,f);(i,c);(a,b);(c,f);(i,g);(i,h);(c,d);(a,h);(b,c);(d,e);(f,e);(b,h);(d,f)}

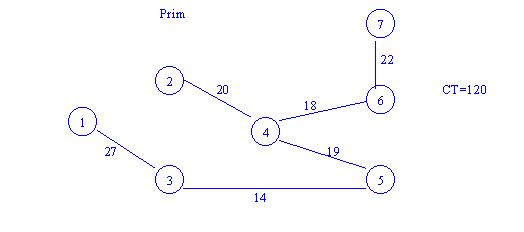
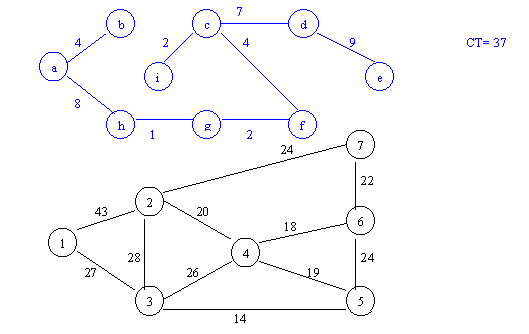
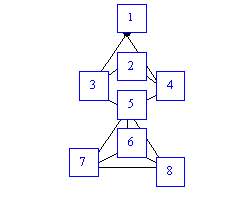
Kruscal:

{(3,5);(4,6);(4,5);(2,4);(6,7);(2,7);(5,6);(3,4);(1,3);(2,3);(1,2)}