Geometría Analítica

 
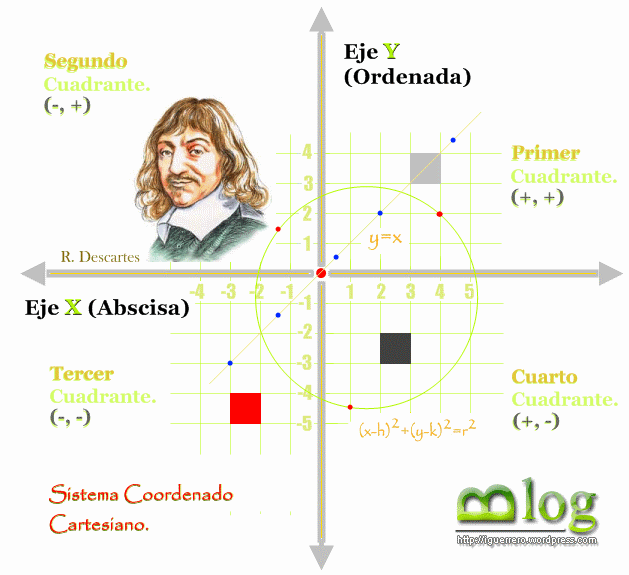
      La geometría analítica estudia las figuras geométricas mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Su desarrollo histórico comienza con la geometría cartesiana, impulsada con la aparición de la geometría diferencial de Carl Friedrich Gauss y más tarde con el desarrollo de la geometría algebraica. Actualmente la geometría analítica tiene múltiples aplicaciones más allá de las matemáticas y la ingeniería, pues forma parte ahora del trabajo de administradores para la planeación de estrategias y logística en la toma de decisiones.

      Las dos cuestiones fundamentales de la geometría analítica son:

      Dado el lugar geométrico en un sistema de coordenadas, obtener su ecuación.
Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que verifican dicha ecuación.

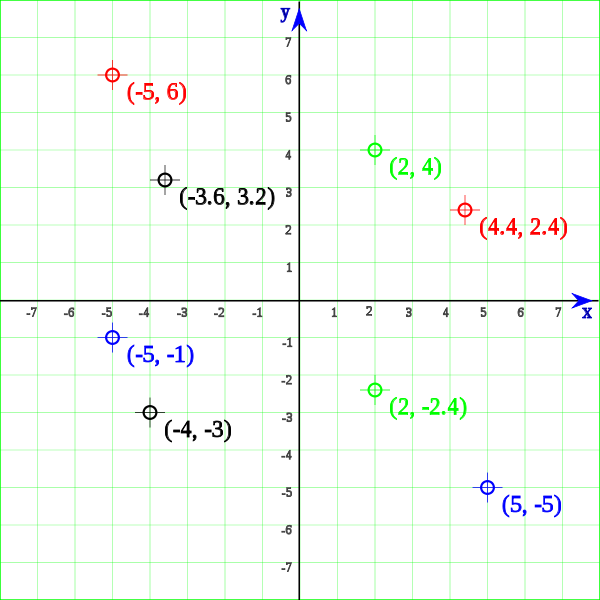
      En un sistema de coordenadas cartesianas, un punto del plano queda determinado por dos números, llamados abscisa y ordenada del punto. Mediante ese procedimiento a todo punto del plano corresponden siempre dos números reales ordenados (abscisa y ordenada), y recíprocamente, a un par ordenado de números corresponde un único punto del plano. Consecuentemente el sistema cartesiano establece una correspondencia biunívoca entre un concepto geométrico como es el de los puntos del plano y un concepto algebraico como son los pares ordenados de números. Esta correspondencia constituye el fundamento de la geometría analítica.

      Con la geometría analítica se puede determinar figuras geométricas planas por medio de ecuaciones e inecuaciones con dos incógnitas. Éste es un método alternativo de resolución de problemas, o cuando menos nos proporciona un nuevo punto de vista con el cual poder atacar el problema.

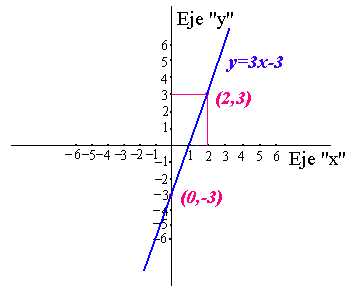     Una recta es el lugar geométrico de todos los puntos en el plano tales que, tomados dos cualesquiera de ellos, el cálculo de la pendiente resulta siempre igual a una constante.

        La ecuación general de la recta es de la forma:  Ax + By + C = 0

cuya pendiente es m = -A/B y cuya ordenada al origen es b = -C/B.

     Una recta en el plano se representa con la Función lineal de la forma: 
y = mx + b

 

1)    Demostrar que los puntos A(0,1), B(3,5), C(7,2), D(4,-2) son los vértices de un cuadrado.

 

2)    Dos de los vértices de un triángulo equilátero son A(-1,1) y B(3,1). Hallar las coordenadas del otro vértice. (2 casos)

 
3)    Determinar las coordenadas de los extremos C y D que es dividido en tres partes iguales por los puntos A(2,2) y B(5,2).

 

4)    Tres de los vértices de un paralelogramo son A(-1,4), B(1,-1) y C(6,1). Si la ordenada del cuarto vértice es 6 ¿Cuál es su abscisa?

 
5)    ¿Hasta qué punto debe prolongarse el segmento que une los puntos A(0,0) y B(3,4) en la dirección AB, para que su longitud se duplique?