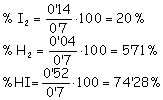En un recipiente de un litro de capacidad se introducen 0’4 moles de yoduro de hidrógeno, 0’2 moles de yodo y 0’1 moles de hidrógeno. La KC para la descomposición del yoduro de hidrógeno ajustada a dos moles descompuestos, vale 2’07.10-2 mol/l a una temperatura de 1000oK.

        a)  Discuta razonadamente hacia dónde se desplazará la reacción para alcanzar

             el equilibrio.

        b)  Calcule el porcentaje que hay de cada gas en el equilibrio.

        c)  Calcule la presión parcial de cada gas en el equilibrio y la Kp.

        d)  Si para el mismo equilibrio, inicialmente sólo se hubiesen introducido 64 g

             de yoduro de hidrógeno, ¿qué tanto por ciento quedaría sin disociar una

     vez alcanzado el equilibrio?. ¿Cuánto valdrá el grado de disociación?

        e)  Discuta y Justifique la evolución del equilibrio si:

                e.1)  Se disminuye la temperatura (la descomposición es exotérmica)

                e.2)  Se añade yodo.

                e.3)  Se añade al recipiente un gas noble (que no reacciona)

                e.4)  Se añade un catalizador.

        (Masas atómicas: I = 127 ; H = 1)

 a)    , por lo tanto, para alcanzar el valor de Kc la expresión de Q deberá disminuir. Para que un conciente disminuya debe disminuir su numerador(productos) y aumentar su denominador (reactivos). Eso supone un desplazamiento a la izquierda.

b) 

3’31.10^-3 + 0’083 x² + 0’0331 x = x² – 0’3 x + 0’02

0 = 0’917 x² – 0’3331 x + 0’0167

x₁ = 0’3031 (no es válida; no puede reaccionar más de lo que hay)

x₂ = 0’06 Õ válida

Por lo tanto:

            [I₂]= 0’2 – 0’06 = 014 moles/litro

            [H₂] = 0’1 – 0’06 = 0’04 moles /litro   

            [HI]= 0’4 + 2 . 0’06 = 0’52

c) 

         Pp I₂ = 0’2 . 57’4 = 11’48  atm ;  Pp H₂ = 0’571 . 57’4 = 32’77 atm ;

Pp HI = 0’743 . 57’4 = 42’64 atm

d)

a = (2 - 2a) . 0’144 = 0’288 – 0’288 a

1’288 a = 0’288  Õ 

Quedará, por tanto, un 77’7 %

e)  Según el principio de LeChatelier que dice que ante una perturbación el equilibrio siempre reacciona compensando dicha perturbación se puede decir que:

            1)  Si se disminuye la temperatura el equilibrio tenderá a aumentarla desplazándose en sentido exotérmico, es decir, hacia la derecha.

            2)  Si se añade I₂, el equilibrio tenderá a consumirlo lo que implica un desplazamiento hacia la izquierda para alcanzar un nuevo equilibrio.

            3)  Si se añade un gas noble no reactivo, el efecto es el mismo que si se aumenta la presión, pues ésta es indiferente al tipo de sustancia gaseosa. Por lo tanto el equilibrio se desplazaría en el sentido en el que se produzca un menor número de moles, sentido que no existe en el equilibrio que nos ocupa. Por lo tanto el equilibrio no se desplaza.

            4)  El catalizador aumenta la velocidad en los dos sentidos, por lo que el equilibrio no se ve alterado.