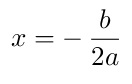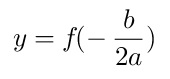Vértice de una parábola
Es el punto de la parábola donde ella alcanza su máximo o mínimo con respecto al eje Y.
Si la parábola es cóncava hacia abajo, el vértice es el punto más alto en la gráfica de la función
cuadrática y si la parábola es cóncava hacia arriba, el vértice es el punto más bajo en la gráfica de
la función.
|

| 
|
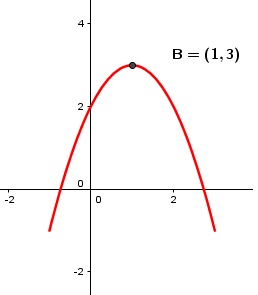
Figura 7
| Figura 8
| |
La coordenada X del vértice se obtiene con la siguiente ecuación:
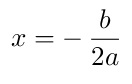
|
La coordenada Y del vértice se obtiene sustituyendo la coordenada x calculada con
la expresión anterior y sustituyéndola en la función de la parábola correspondiente de la
siguiente manera:
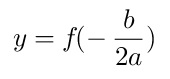
La función de la Figura 7 es f(x) = x²+4x+3 y el de la Figura 8 es f(x) = -x²+2x+2.
Te invito a que verifiques las coordenadas de los vértices ahí graficados utilizando el procedimiento
anterior.
|
<
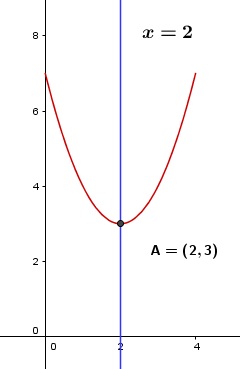
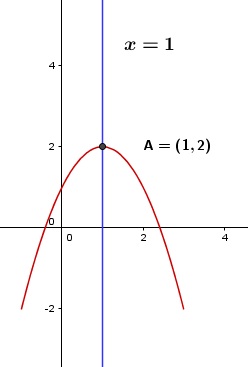
Eje de Simetría
El Eje de Simetría de una parábola es una recta paralela al eje Y, que pasa por el
vértice y que la divide en dos partes igual. En la Figura 9 y Figura 10 que aparecen
más abajo, te ilustramos esto. |
| 
|
Figura 9
| Figura 10
| |
Para complementar tu aprendizaje, te invito a ingresar a la página de ejercicios, haciendo click en bob esponja!
|

Página 1
2 3
4
|