Función Cuadrática

Una Funcion Cuadrática es una función de la forma

o bien

donde a, b, c son constantes (a distinto de 0), "x" la variable independiente e "y" la variable dependiente. La gráfica de una función cuadrática se denomina Parábola. Si la constante a > 0 la parábola se abrirá hacia arriba como muestra la figura 1. mientras que si a < 0 la parábola se abrirá hacia abajo como muestra la figura 2.


Figura 1	Figura 2

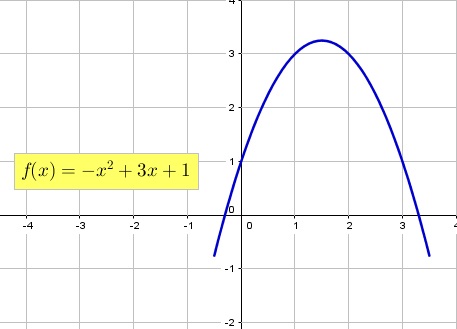
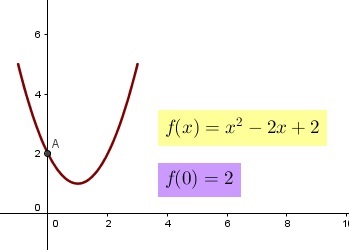
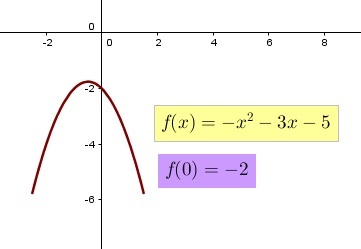
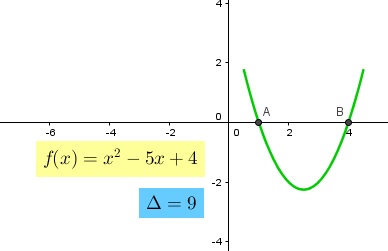
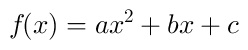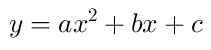Intersecciones

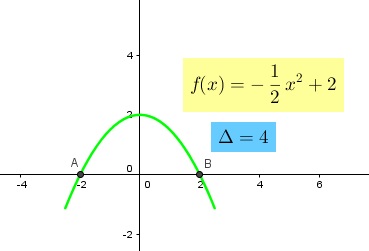
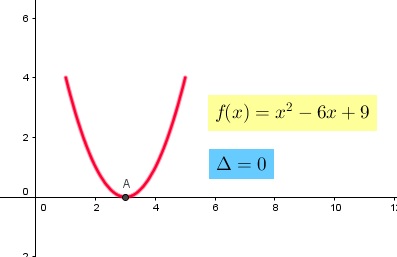
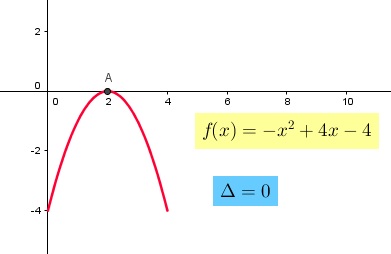
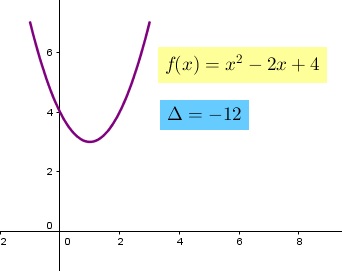
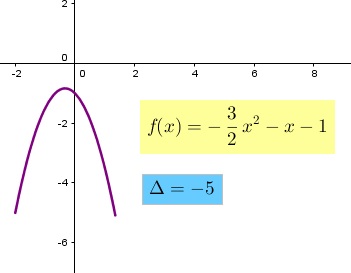
La intersección de la parábola con el eje "y" es el punto (0,c), donde c = f(0). Para determinar si la parábola intersecta al eje "x" se debe calcular su determinante y analizar el valor como se menciono anteriormente. En el caso que existan dos soluciones distintas, significa que la parábola corta al eje "x" en dos puntos. 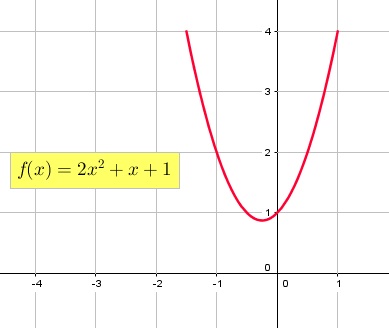Si existen dos soluciones iguales, la parábola intersecta sólo en un punto al eje "x" y por último si no existen soluciones la parábola no corta al eje "x". En las Figuras 3, 4, 5 y 6 se muestra de manera gráfica el análisis descrito anteriormente. En el caso de existencia de soluciones, para encontrarlas, se debe resolver la ecuación f(x) = 0, la cual es una ecuación cuadrática viste en la página anterior. Con esta ecuación se encuentran los valores de x, tales que la imagen de la función es cero.


Figura 3: En ambas figuras el punto A corresponde a la intersección de la parábola con el eje Y, cuyo corte se produce en f(0).

Figura 4: En ambas figuras los puntos A y B corresponden a la intersección de la parábola con el eje X. En ambos casos el discriminante de la función es positivo.

Figura 5: En ambas figuras el punto A corresponde a la única intersección de la parábola con el eje X. En ambos casos el driscriminante de la función es cero.

Figura 6: En ambas figuras no existe un punto de intersección entre la parábola y el eje X. En ambos casos el discriminante de la función es negativo.

Página 1 2 3 4