| Ecuación Cuadrática La ecuación cuadrática es una ecuación formada por la suma algebraica de términos en donde al menos uno de ellos tiene la variable elevada al exponente 2. Es decir, es una expresión como la que te mostramos a continuación: 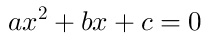 donde x es la variable, y a, b, c constantes; a es el coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente. |
|
Solución de una Ecuación Cuadrática Para una Ecuación Cuadrática con coeficientes reales pueden existir dos soluciones, no necesariamente distintas o pueden no existir. Si las soluciones existen las llamaremos raíces de la ecuación, las cuales pueden ser reales o complejas. La fórmula que permite calcular las soluciones de la ecuación, en caso que existan, es la siguiente: 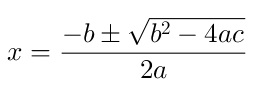 O podemos expresarla de una manera más práctica para entenderla mejor como sigue: 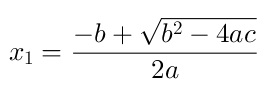
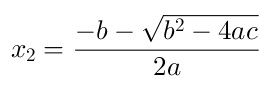 |
En la fórmula para el cáculo de soluciones, la expresión 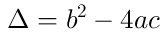 recibe el nombre de discriminante de la ecuación cuadrática. Dependiendo del valor de ésta expresión, se pueden dar las siguientes situaciones con respecto a la existencia de las soluciones: 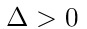 La ecuación tiene dos soluciones distintas y reales. La ecuación tiene dos soluciones distintas y reales. 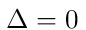 La ecuación tiene dos soluciones iguales y reales. La ecuación tiene dos soluciones iguales y reales. 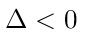 La ecuación no tiene soluciones reales. Sus soluciones son números complejos. La ecuación no tiene soluciones reales. Sus soluciones son números complejos. |